Ngọc Sơn Bùi Văn Cường

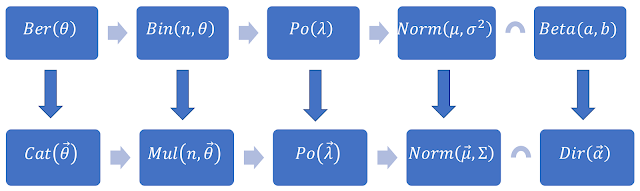
Kết thúc loạt bài viết nói về quan hệ giữa các phân phối xác suất thông dụng nhất, cũng như vài thủ thuật nhớ những thứ liên quan, trong bài viết cuối này, tôi sẽ nói về 2 phân phối xác suất có quan hệ với Gaussian 1 chiều và Gaussian nhiều chiều. Nhưng, chúng không phải quan hệ tổng quát hóa như những bài trước, vì 2 phân phối này biểu diễn loại biến ngẫu nhiên khác với các phân phối trước! Beta và Dirichlet là 2 phân phối xác suất tương ứng cho với trường hợp biến ngẫu nhiên 1 chiều và nhiều chiều. Dirichlet là phân phối tổng quát của Beta. Khi nghiên cứu, về chúng, bạn sẽ biết được rằng 2 phân phối này dùng để mô tả biến động  cho các tham số của những phân phối xác suất tương ứng mà chúng  liên hợp . Quan hệ với Gaussian. Ở đây xuất hiện khái niệm phân phối liên hợp . Nếu bạn chưa hiểu thế nào là 2 phân phối xác suất liên hợp nhau thì có thể hiểu theo cách đơn giản rằng khi đem nhân 2 kernel của chúng với nhau, ta thu được kết quả có hình dạng tương tự với cả 2 k...

Ngày cuối Thu năm ấy, hắn 24+ tuổi. Vào cái năm đó, cái năm mà hắn đi hết từ mảng này đến mảng khác, tu vi tăng tiến vượt bậc; nhưng cũng đi hết từ dự định này đến dự định khác; thì Hà Nội cũng thăng trầm ko kém. Nửa đầu năm, trước 1 tổng giám đốc, 1 huyền thoại võ lâm IT, hắn đã nghĩ rằng Engineering mới là đích thực. Trong cái ngành Security này, chỉ có làm nhiều thì mới tìm ra nhiều vấn đề thiết thực; có học tiếp lên nữa cũng ko đóng góp nhiều tích lũy cho bản thân. Trong quá trình làm việc, hắn ko ngừng tự học Toán, hơn nữa còn học nhiều và đọc nhiều để thỏa mãn bản thân.  Lúc đó, Hà Nội đón Donald Trump và Kim Jong Un, trở thành nơi được tín nhiệm bậc nhất thế giới. Việt Nam trở thành Ủy viên ko thường trực Hội đồng bảo an Liên Hợp Quốc, trở thành đất nước được tín nhiệm bậc nhất thế giới. Việt Nam ký được những thỏa thuận, hợp tác mà ko có nước nào ở ASEAN ký được. Đội tuyển bóng đá thì luôn làm thỏa mãn người hâm mộ nói riêng và người dân Việt Nam nói chung; là 1 ...

Hôm qua, Sư Phụ hẹn tôi lên nói chuyện về dự định đồ án cũng như nghiên cứu. Đồ án thì xong từ thời cổ lỗ sĩ rồi, chủ yếu là công việc nghiên cứu. Ngoài ra cũng có mấy cậu sv năm cuối được hẹn lên gặp để làm đồ án tốt nghiệp. Qua cuộc nói chuyện giữa Sư Phụ và các cậu sv đó, Sư Phụ đã chỉ ra 2 sai lầm của mọi người về mặt tư tưởng rằng: AI/Machine Learning cũng chỉ là 1 phần trong 1 kỹ sư  thôi, và cũng ko phải là phần cốt lõi tạo nên chất  của kỹ sư đó! Đừng vì nó hot mà cố tìm cách sử dụng nó để tạo ra thứ mà ko ai cần! Kỹ sư  ko phải loại người  mà hầu hết xã hội (thị trường lao động) đang nghĩ! Quá lạm dụng từ "kỹ sư"  đẫn đến xã hội hiểu và đánh giá sai vai trò của 1 người thực sự là kỹ sư . Về điều đầu tiên, hiển nhiên rồi! Trong vài năm gần đây, AI (Artificial Intelligence) - hay còn gọi là "trí tuệ nhân tạo" - là từ khóa hot nhất trong ngành. Hot đến nỗi các bác nông dân ở quê cũng biết có thuật ngữ này tồn tại. Nhưng thật sự thì như vậy là ha...

Trong bài viết trước, tôi đã trình bày về việc xấp xỉ Binomial về Poisson (khi xác suất thành công rất hiếm) và về Gaussian (khi xác suất thành công ko hề hiếm). Việc chứng minh về căn bản cũng ko dùng nhiều kiến thức Toán cao cấp lắm, hầu như vẫn chỉ cần dùng kiến thức Toán ở bậc THPT là có thể hiểu được (mệt cái là gõ Latex hơi lắm thôi). Tiếp tục seri bài viết, trong bài viết này, tôi sẽ tiếp tục tổng quát hóa phân phối Poisson về Gaussian. Khi đã tới được Gaussian rồi, một loạt các phân phối xác suất mới sẽ xuất hiện theo, vì chúng đều xuất phát từ việc lấy mẫu dựa trên Gaussian. Poisson sẽ tiến về Gaussian. Nếu đi từ Binomial, khi $\lambda=n.\theta$ tiến đến vô hạn, Binomial sẽ tiến về Gaussian. Tuy nhiên, nếu ko đi từ Binomial, mà đi từ Poisson thì sao. Sẽ ra sao khi $\lambda$ của Poisson tiến đến $+\infty$? Ừ thì có thể coi rằng khi $\lambda\to+\infty$, đồng nghĩa với việc $n\to+\infty$ (vì $\theta\le1$ bị giới hạn; nếu như $\theta$ không quá nhỏ (hoặc ko quá lớn), ...

"Trung thu trăng sáng như gương". Trung thu j mà người lớn ăn cỗ hát kara, trẻ em thì replay n lần cái bài hát láo toét "độ ta ko độ nàng". May quá 11h đêm cũng yên ắng đi đc. Tiếp nối bài viết lần trước, trong bài này, tôi sẽ tiếp tục nói về quan hệ biến đổi qua lại lẫn nhau giữa các phân phối xác suất thông dụng nhất trong quá trình tìm hiểu về Machine Learning. Bài viết này tôi phải gõ latex khá nhiều, do đó nếu chẳng may có sai sót ở ký tự toán học nào thì mong các bạn góp ý để sửa lại cho chính xác. Trong bài viết trước, chúng ta đã dừng lại ở phân phối Binomial (nhị thức) với loại biến ngẫu nhiên 1 chiều, phân phối Multinomial với loại biến ngẫu nhiên nhiều chiều. Tiếp ngay sau đây, chúng ta sẽ thảo luận về cách biến hình từ phân phối Binomial về phân phối Poisson. Tôi cũng xin nói luôn rằng tôi sẽ ko thảo luận sâu về phân phối Poisson nhiều chiều $Po(\vec{\lambda})$; lý do là vì tôi chưa gặp phân phối Poisson nhiều chiều trong thực tế quá trình t...

Hôm nay đi nhậu chia tay 1 ông anh đồng nghiệp đồng hương, uống hơi nhiều nên khá sấp và ko về nhà được, mấy ae đành lên công ty ngủ lại vs 2 bro trực hệ thống SOC ban đêm. Tuy nhiên do uống chưa đủ để sấp thực sự nên lại như mọi khi: "ko buồn ngủ". Vậy là ngẫu hứng dậy mở máy viết bài này.  Bài viết này, tôi chỉ giới thiệu qua loa về một vài phân phối xác suất thông dụng cũng như tương quan giữa chúng. Chúng ta sẽ gặp những phân phối xác suất này rất nhiều trong quá trình nghiên cứu về Machine Learning. Còn tương quan giữa chúng chính là cách mà phân phối này có thể trở thành phân phối kia với những điều kiện cho trước nào đó.  Vì sao lại là phân phối xác suất ? Đơn giản thôi, trong tự nhiên, mọi biến cố ngẫu nhiên (ví dụ như khả năng bạn cười 1 ai đó trong 1 tập các em gái cho trước) đều có thể thống kê. Nếu như nó tuân theo 1 phân phối xác suất nào đó (phổ điểm thi đại học tuân theo phân phối chuẩn) thì ta có thể dễ dàng đánh giá biến cố đó dựa vào đặc tính sẵn ...

Tâm sự. Như tôi đã từng viết, đối với tôi, Toán học là thứ nội công tuyệt hảo nhất. Một kỹ sư tin học mà ko biết Toán thì cảnh giới của anh ta rồi cũng sẽ chỉ tiến sát đến 1 mốc cố định, và ko thể nào đột phá thêm được nữa. Nhưng, Toán rất khó, tôi cũng ko giỏi Toán; thế nên tôi luôn nể phục những người giỏi Toán. Khi gặp phải 1 vấn đề Toán học khó mà mãi ko hiểu, tôi thường có những giây phút bi quan rằng "ước j mình giỏi Toán như bọn đi thi IMO, như các thầy dạy Toán ở trường BK, ... Phải chi khá hơn 1 chút nữa thôi thì mình học cái j mới cũng sẽ nhanh hơn.".  Đó là những bút tích còn sót lại 1 thời học sinh mê Toán 1 cách nghiệp dư của tôi. Đối vs tôi, chỉ với tôi thôi, đó là những phát kiến vĩ đại của bản thân.  Hồi cấp 1. Tôi thích Toán từ ngày học lớp 3. Tôi nhận ra điều này khi mà đang rất buồn ngủ sau khi vừa viết xong 1 bài Tập làm văn thì tự nhiên tỉnh ngủ hẳn sau khi giải xong 1 bài Toán. Tôi kể điều đó với Mẹ, Mẹ tôi khuyên rằng hãy theo Toán. Khoản...