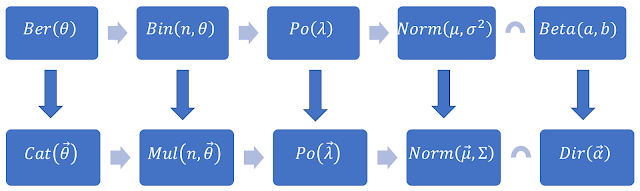
Quan hệ giữa các phân phối xác suất thông dụng nhất: Từ Binomial cho đến Poisson và Gaussian.

"Trung thu trăng sáng như gương". Trung thu j mà người lớn ăn cỗ hát kara, trẻ em thì replay n lần cái bài hát láo toét "độ ta ko độ nàng". May quá 11h đêm cũng yên ắng đi đc.

Tiếp nối bài viết lần trước, trong bài này, tôi sẽ tiếp tục nói về quan hệ biến đổi qua lại lẫn nhau giữa các phân phối xác suất thông dụng nhất trong quá trình tìm hiểu về Machine Learning. Bài viết này tôi phải gõ latex khá nhiều, do đó nếu chẳng may có sai sót ở ký tự toán học nào thì mong các bạn góp ý để sửa lại cho chính xác.

Trong bài viết trước, chúng ta đã dừng lại ở phân phối Binomial (nhị thức) với loại biến ngẫu nhiên 1 chiều, phân phối Multinomial với loại biến ngẫu nhiên nhiều chiều. Tiếp ngay sau đây, chúng ta sẽ thảo luận về cách biến hình từ phân phối Binomial về phân phối Poisson. Tôi cũng xin nói luôn rằng tôi sẽ ko thảo luận sâu về phân phối Poisson nhiều chiều $Po(\vec{\lambda})$; lý do là vì tôi chưa gặp phân phối Poisson nhiều chiều trong thực tế quá trình tự học bao giờ. Trước khi nảy ra ý định viết bài này, tôi cũng đã Google search qua về phân phối Poisson cho biến ngẫu nhiên nhiều chiều, nhưng trong quá trình đọc thì thấy họ có nói rằng phân phối Poisson nhiều chiều này ít gặp trong thực tế nghiên cứu thống kê. Do vậy, từ bây giờ, khi nói về phân phối Poisson, ta chỉ hiểu rằng đó là phân phối Poisson cho biến ngẫu nhiên 1 chiều. (Các bạn có hứng thú tìm hiểu có thể đọc qua paper này, cũng khá chi tiết).

Ở bài viết trước, chúng ta đã biết rằng phân phối Binomial mô phỏng xác suất thành công trong việc thu được $k$ mặt ngửa trong $n$ lần tung đồng xu. Vậy còn tổng quát được hơn? Đương nhiên rồi, Binomial chỉ có thể mô phỏng được việc tung đồng xu với số $n$ lần xác định và hữu hạn. Vậy khi ta tung đồng xu vô hạn lần thì sao? Khi ta tung vô hạn lần, tương đương với việc $n$ sẽ là $+\infty$, vậy thì ta làm sao có thể tính được xác suất chỉ có đúng $k$ lần xuất hiện mặt ngửa được? Tung vô hạn lần cơ mà, tôi cứ tung cho đến khi nào xuất hiện mặt ngửa lần thứ $k$; ai dám chắc rằng sẽ ko bao giờ tung ra mặt ngửa nữa nếu cứ tiếp tục tung tiếp? 

Từ đó, ko biết tại vì sao, ông Poisson lại nghĩ ra 1 phân phối xác suất mới hay đến vậy. Đọc Wiki hay Google search, bạn sẽ thấy rằng phân phối Poisson cần thông tin đầu vào là trung bình số lần thành công của 1 phép thử trong 1 đơn vị thời gian nhất định, chứ ko phải là số lần thực hiện phép thử $n$ hay xác suất thành công $\theta$ của mỗi lần thực hiện phép thử. Phân phối Binomial có thể xấp xỉ về phân phối Poisson khi $n$ đủ lớn và $\theta$ đủ nhỏ. Vậy làm sao để biến hình từ phân phối Binomial về dạng phân phối Poisson, bạn có thể đọc đoạn biến đổi sau đây nếu ko ngại, thực ra biến đổi ko có j quá khó hiểu, toàn kiến thức THPT thôi.

Theo ta biết:

• Phân phối Binomial có hàm mật độ khối: $Bin(k|n,\theta)=\binom{n}{k}.\theta^k.(1-\theta)^{n-k}=C^{k}_{n}.\theta^k.(1-\theta)^{n-k}$
• Phân phối Poisson có hàm mật độ khối: $Po(k|\lambda)=e^{-\lambda}.\frac{\lambda^k}{k!}$

Vì $n$ rất lớn và $\theta$ đủ nhỏ, nên tích $n.\theta$ sẽ là 1 hằng số hữu hạn, đặt $\lambda=n.\theta$, ta sẽ biến đổi xuất phát từ Binomial như sau:

\[Bin(k|n,\theta)=C^{k}_{n}.\theta^k.(1-\theta)^{n-k}=\frac{n!}{k!.(n-k)!}.\theta^k.(1-\theta)^{n-k}\]

\[=\frac{n!}{k!.(n-k)!}.\frac{\lambda^k}{n^k}.(1-\frac{\lambda}{n})^{n-k}=\frac{n!}{n^k.(n-k)!}.\frac{\lambda^k}{k!}.(1-\frac{\lambda}{n})^n.(1-\frac{\lambda}{n})^{-k}\]

Khi $n\to\infty$, ta có giới hạn sau của hàm Binomial trên:

\[\mathop {\lim }\limits_{n \to \infty }Bin(k|\lambda )=\mathop {\lim }\limits_{n \to \infty }\left[ {\frac{n!}{n^k.(n-k)!}.\frac{\lambda^k}{k!}.(1-\frac{\lambda}{n})^n.(1-\frac{\lambda}{n})^{-k}} \right]\]
Đánh giá qua 1 chút, ta thấy rằng:
\[\frac{{n!}}{{{n^k}.(n - k)!}} < \frac{{n!}}{{\left( {n - k + 1} \right)...\left( {n - k + k} \right).\left( {n - k} \right)!}} < \frac{{n!}}{{n!}} = 1\]
\[\mathop {\lim }\limits_{n \to \infty } {\left( {1 - \frac{1}{n}} \right)^{ - k}} = {1^{ - k}} = 1\]
Đương nhiên, 2 dòng biến đổi trên mới chỉ là đánh giá qua thôi, còn thật ra nếu chặt chẽ, chúng ta phải chứng minh kết quả đánh giá của biến đổi bên trên, còn giới hạn bên dưới thì chặt chẽ rồi:

• Bổ đề: Chứng minh $\mathop {\lim }\limits_{n \to \infty } \frac{{n!}}{{{n^x}.\left( {n - x} \right)!}} = 1$

Chứng minh bổ đề này cũng ko có j khó quá, vẫn chỉ là kiến thức THPT:
\[\mathop {\lim }\limits_{n \to \infty } \frac{{n!}}{{{n^x}.\left( {n - x} \right)!}} = \mathop {\lim }\limits_{n \to \infty } \frac{{\left( {n - x} \right)!.\left( {n - x + 1} \right)\left( {n - x + 2} \right)...\left( {n - x + x} \right)}}{{\left( {n - x} \right)!.{n^x}}}\]
\[ = \mathop {\lim }\limits_{n \to \infty } \frac{{\left( {n - x + 1} \right)\left( {n - x + 2} \right)...\left( {n - x + x} \right)}}{{{n^x}}} = \mathop {\lim }\limits_{n \to \infty } \left[ {\left( {\frac{{n - x + 1}}{n}} \right)\left( {\frac{{n - x + 2}}{n}} \right)...\left( {\frac{{n - 1}}{n}} \right).\frac{n}{n}} \right]\]
\[ = \mathop {\lim }\limits_{n \to \infty } \left[ {1.\left( {1 - \frac{1}{n}} \right)\left( {1 - \frac{2}{n}} \right)...\left( {1 - \frac{{x - 2}}{n}} \right)\left( {1 - \frac{{x - 1}}{n}} \right)} \right] = 1\]
Do đó, giới hạn trên trở thành:
\[\mathop {\lim }\limits_{n \to \infty } Bin(k|\lambda  ) = \mathop {\lim }\limits_{n \to \infty } \left[ {\frac{{{\lambda ^k}}}{{k!}}.{{\left( {1 - \frac{\lambda }{n}} \right)}^n}} \right] = \frac{{{\lambda ^k}}}{{k!}}.\mathop {\lim }\limits_{n \to \infty } \left[ {{{\left( {1 - \frac{\lambda }{n}} \right)}^n}} \right]\]
Well well well, ta vướng phải 1 giới hạn mà hệ quả của nó được sử dụng ở cấp THPT như 1 định lý thừa nhận ko chứng minh: $\mathop {\lim }\limits_{n \to \infty } {\left( {1 + \frac{1}{n}} \right)^n} = e$
Và dạng tổng quát hơn của nó là đây: $\mathop {\lim }\limits_{n \to \infty } {\left( {1 - \frac{\lambda }{n}} \right)^n} = {e^{ - \lambda }}$
Kể ra thì việc chứng minh định lý này có sử dụng đến tư tưởng của Chuỗi số mà các bạn sinh viên sẽ được học ở môn Giải tích của Toán cao cấp; nhưng nếu muốn chứng minh để hiểu nó ở mức THPT cũng ko phải là bất khả thi. Hồi lớp 12, sau khi học xong Đạo hàm, Thầy mình cũng có 1 lần nói về chuỗi khai triển Taylor của 1 đa thức bất kỳ, đó là hệ quả của việc khai triển Taylor 1 hàm số bất kỳ về dạng 1 đa thức bậc $n$ bao nhiêu cũng được. Sau này mình dùng nó để tính tích phân thôi chứ ko có j đặc sắc hơn. Bây giờ, ta sẽ dùng dạng chuẩn tắc của nó, là khai chiển Maclaurin để giải quyết định lý trên; nhưng chúng ta chỉ dùng nó 1 tí ti ở cuối thôi, còn hầu hết toàn bộ biến đổi, chúng ta vẫn chỉ cần dùng kiến thức THPT để hiểu!

• Bổ đề: chứng minh $\mathop {\lim }\limits_{n \to \infty } {\left( {1 - \frac{\lambda }{n}} \right)^n} = {e^{ - \lambda }}$

Đầu tiên, chúng ta sẽ sử dụng nhị thức Newton để khai triển biểu thức mũ trong phép giới hạn:\[{\left( {1 - \frac{\lambda }{n}} \right)^n} = \sum\limits_{k = 0}^n {\left( \begin{array}{l}
n\\
k
\end{array} \right)} {.1^k}.{\left( {\frac{{ - \lambda }}{n}} \right)^{n - k}} = \sum\limits_{k = 0}^n {C_n^k{{.1}^k}.{{\left( {\frac{{ - \lambda }}{n}} \right)}^{n - k}}} \]
\[ = C_n^0{.1^n}.{\left( {\frac{{ - \lambda }}{n}} \right)^0} + C_n^1{.1^{n - 1}}.{\left( {\frac{{ - \lambda }}{n}} \right)^1} + C_n^2{.1^{n - 2}}.{\left( {\frac{{ - \lambda }}{n}} \right)^2} + C_n^3{.1^{n - 3}}.{\left( {\frac{{ - \lambda }}{n}} \right)^3} + ...\]
\[ = 1 + n.\left( {\frac{{ - \lambda }}{n}} \right) + \frac{{n\left( {n - 1} \right)}}{{2!}}.{\left( {\frac{{ - \lambda }}{n}} \right)^2} + \frac{{n\left( {n - 1} \right)\left( {n - 2} \right)}}{{3!}}.{\left( {\frac{{ - \lambda }}{n}} \right)^3} + ...\]
\[ = 1 - \lambda  + \frac{{{\lambda ^2}}}{{2!}}.\frac{{n - 1}}{n} - \frac{{{\lambda ^3}}}{{3!}}.\frac{{\left( {n - 1} \right)\left( {n - 2} \right)}}{{{n^2}}} + \frac{{{\lambda ^4}}}{{4!}}.\frac{{\left( {n - 1} \right)\left( {n - 2} \right)\left( {n - 3} \right)}}{{3!}} - ...\]
\[ = 1 - \lambda  + \frac{{{\lambda ^2}}}{{2!}}.\left( {1 - \frac{1}{n}} \right) - \frac{{{\lambda ^3}}}{{3!}}.\left( {1 - \frac{1}{n}} \right).\left( {1 - \frac{2}{n}} \right) + \frac{{{\lambda ^4}}}{{4!}}.\left( {1 - \frac{1}{n}} \right)\left( {1 - \frac{2}{n}} \right)\left( {1 - \frac{3}{n}} \right) - ...\]
Đem ốp kết quả trên vào giới hạn chứng minh, ta được:
\[\mathop {\lim }\limits_{n \to \infty } {\left( {1 - \frac{\lambda }{n}} \right)^n} = \mathop {\lim }\limits_{n \to \infty } \left[ {1 - \lambda  + \frac{{{\lambda ^2}}}{{2!}}.\left( {1 - \frac{1}{n}} \right) - \frac{{{\lambda ^3}}}{{3!}}.\left( {1 - \frac{1}{n}} \right).\left( {1 - \frac{2}{n}} \right) + \frac{{{\lambda ^4}}}{{4!}}.\left( {1 - \frac{1}{n}} \right)\left( {1 - \frac{2}{n}} \right)\left( {1 - \frac{3}{n}} \right) - ...} \right]\]
\[ = 1 - \lambda  + \frac{{{\lambda ^2}}}{{2!}}.\mathop {\lim }\limits_{n \to \infty } \left( {1 - \frac{1}{n}} \right) - \frac{{{\lambda ^3}}}{{3!}}.\mathop {\lim }\limits_{n \to \infty } \left( {1 - \frac{1}{n}} \right).\left( {1 - \frac{2}{n}} \right) + \frac{{{\lambda ^4}}}{{4!}}.\mathop {\lim }\limits_{n \to \infty } \left( {1 - \frac{1}{n}} \right)\left( {1 - \frac{2}{n}} \right)\left( {1 - \frac{3}{n}} \right) - ...\]
\[ \Leftrightarrow \mathop {\lim }\limits_{x \to \infty } {\left( {1 - \frac{\lambda }{n}} \right)^n} = 1 - \lambda  + \frac{{{\lambda ^2}}}{{2!}} - \frac{{{\lambda ^3}}}{{3!}} + \frac{{{\lambda ^4}}}{{4!}} - ...\]
Vế phải của kết quả trên chính là khai triển Maclaurin của hàm số $y(\lambda)=e^{-\lambda}$. Do đó ta được kết quả:
\[\mathop {\lim }\limits_{x \to \infty } {\left( {1 - \frac{\lambda }{n}} \right)^n} = {e^{ - \lambda }}\]
Ốp tất cả các kết quả trên vào giới hạn của hàm mật độ khối xác suất, ta thấy giới hạn trên trở thành:
\[\mathop {\lim }\limits_{n \to \infty } Bin(k|\lambda  ) = \frac{{{\lambda ^k}}}{{k!}}.{e^{ - \lambda }}=Po(k|\lambda)\]
Kết quả ở vế phải của giới hạn trên chính là công thức của hàm mật độ (khối) xác suất của phân phối Poisson. Vậy là phân phối Binomial sẽ tiến gần xấp xỉ về phân phối Poisson trong trường hợp số lần tung đồng xu là vô hạn. Ta có thêm 1 lưu ý nhỏ là: xác suất thành công của mỗi lần thực hiện phép thử phải đủ nhỏ! Giả thiết này được đưa vào để đảm bảo $\lambda=n.\theta$ là 1 số hữu hạn khi $n$ tiến ra $+\infty$; chứ nếu $k$ cũng tiến ra $+\infty$ thì độ chính xác của việc xấp xỉ Binomial về Poisson là ko đạt hiệu quả.

Vậy trong trường hợp ko thể kiểm soát để $\theta$ đủ nhỏ? Lúc này, Binomial sẽ ko hội tụ về Poisson nữa, mà sẽ hội tụ về Gaussian. Ta sẽ bàn điều này ngay sau đây. Nhưng trước khi bàn về việc Binomial hội tụ về Gaussian, ta cần nhìn lại định hướng 1 chút:

• Lấy mẫu $X\sim Bin(x|n,p,q=1-p)=C_n^x.p^x.q^{n-x}$ có kỳ vọng $E(X)=np$ và phương sai $V(X)=npq$
• Lấy mẫu $N{\rm{or}}m\left( {x|\mu ,{\sigma ^2}} \right) = \frac{1}{{\sqrt {2\pi {\sigma ^2}} }}\exp \left[ { - \frac{{{{\left( {x - \mu } \right)}^2}}}{{2{\sigma ^2}}}} \right]$ có kỳ vọng $E(X)=\mu$ và phương sai $V(X)=\sigma^2$
• Do đó, để chứng minh Binomial xấp xỉ về Gaussian, ta sẽ chứng minh tương ứng kỳ vọng $np$ với $\mu$ và phương sai $npq$ với $\sigma^2$
• Vấn đề ở đây là làm sao để biến cái tổ hợp trong Binomial kia về dạng hàm số mũ hoặc lũy thừa để ghép với phần còn lại của hàm mật độ. Trong Giải tích, chúng ta có 1 hàm số có thể biến từ giai thừa về hàm mũ và lũy thừa; đó là hàm Gamma: $\Gamma (\alpha ) = \int\limits_0^{ + \infty } {{x^{\alpha  - 1}}{e^{ - x}}dx} $

Nhìn qua chắc nhiều bạn sẽ thắc mắc là với hình dạng thế kia thì hàm Gamma có liên quan j đến giai thừa? Đúng vậy, cứ để nguyên thế kia thì ko thể có j cả; thế nên, ta sẽ dùng tích phân từng phần để biến đổi qua một chút như sau:

• Trước tiên, với $\alpha=1$, ta dễ dàng tính được $\Gamma (\alpha  = 1) = \int\limits_0^{ + \infty } {{x^{1 - 1}}{e^{ - x}}dx}  = \int\limits_0^{ + \infty } {{e^{ - x}}dx}  = 1$
• Với $\alpha>1$, sử dụng phép đặt $\left\{ \begin{array}{l} u = {x^{\alpha  - 1}}\\ dv = {e^{ - x}}dx \end{array} \right.$, lấy tích phân từng phần của hàm Gamma, ta được:

\[\Gamma (\alpha ) = \int\limits_0^{ + \infty } {{x^{\alpha  - 1}}{e^{ - x}}dx}  = uv - \int {v.du}  =  - {x^{\alpha  - 1}}.{e^{ - x}}\left| \begin{array}{l}  + \infty \\ 0 \end{array} \right. + \int\limits_0^{ + \infty } {\left( {\alpha  - 1} \right).{x^{\alpha  - 2}}{e^{ - x}}dx} \]

\[ \Leftrightarrow \Gamma \left( \alpha  \right) = \left( {\alpha  - 1} \right)\int\limits_0^{ + \infty } {{x^{\alpha  - 2}}{e^{ - x}}dx}  = \left( {\alpha  - 1} \right)\Gamma \left( {\alpha  - 1} \right)\]

Do vậy, ta được kết quả: $\Gamma \left( \alpha  \right) = \left( {\alpha  - 1} \right)\Gamma \left( {\alpha  - 1} \right)$

Cứ tiếp tục quy nạp lùi dần dần:

• $\Gamma \left( {\alpha  - 1} \right) = \left( {\alpha  - 2} \right)\Gamma \left( {\alpha  - 2} \right)$
• $\Gamma \left( {\alpha  - 2} \right) = \left( {\alpha  - 3} \right)\Gamma \left( {\alpha  - 3} \right)$
• ... cho đến $\Gamma \left( 1 \right)=1$; và cuối cùng, chúng ta sẽ thu được kết quả:
• $\Gamma \left( \alpha  \right) = \left( {\alpha  - 1} \right)!$ với điều kiện $\alpha$ nguyên dương và $0!=1$

Vậy là đã có thể biến giai thừa về dạng mũ hoặc lũy thừa. Và điều tiếp theo chúng ta cần thực hiện, đó là sử dụng ước lượng Stirling để tính xấp xỉ giai thừa: $\alpha ! \approx \sqrt {2\pi \alpha } {\left( {\frac{\alpha }{e}} \right)^\alpha }$. Tiếp theo, bạn có thể xem cách chứng minh ước lượng Stirling này trên Wolfram. Tuy nhiên tôi thấy việc chứng minh của họ khá ngắn gọn và vắn tắt; do đó bạn có thể đọc tiếp đoạn sau đây nếu muốn xem chứng minh chi tiết.

Theo trên, ta đã thu được kết quả $\alpha ! = \Gamma \left( {\alpha  + 1} \right) = \int\limits_0^{ + \infty } {{x^\alpha }{e^{ - x}}dx}$. Xét biểu thức dưới dấu tích phân, lấy logarit Napier (theo cơ số $e$) rồi thực hiện đạo hàm nó, ta được:

\[\frac{d}{{dx}}\ln \left( {{x^\alpha }{e^{ - x}}} \right) = \frac{d}{{dx}}\left( {\alpha \ln x - x} \right) = \frac{\alpha }{x} - 1 = 0 \Leftrightarrow \alpha  = x\]

Do đó, đặt $x=\alpha+\delta$ với $\delta\ll\alpha$ sẽ là ẩn mới thay thế cho $x$, thay vào biểu thức dưới phép logarit, ta được:

\[\ln \left( {{x^\alpha }{e^{ - x}}} \right) = \alpha \ln \left( {\alpha  + \delta } \right) - \left( {\alpha  + \delta } \right) = \alpha \ln \left[ {\alpha \left( {1 + \frac{\delta }{\alpha }} \right)} \right] - \left( {\alpha  + \delta } \right)\]

\[ = \alpha \left[ {\ln \alpha  + \ln \left( {1 + \frac{\delta }{\alpha }} \right)} \right] - \left( {\alpha  + \delta } \right) = \alpha \left[ {\ln \alpha  + \frac{\delta }{\alpha } - \frac{1}{2}.\frac{{{\delta ^2}}}{{{\alpha ^2}}} + ...} \right] - \left( {\alpha  + \delta } \right)\]

\[ = \alpha \ln \alpha  + \delta  - \frac{{{\delta ^2}}}{{2\alpha }} + ... - \left( {\alpha  + \delta } \right) = \ln {\alpha ^\alpha } - \alpha  - \frac{{{\delta ^2}}}{{2\alpha }}\]

Thực hiện $e$ mũ cả 2 vế của đẳng thức trên, ta được:

\[{x^\alpha }{e^{ - x}} \approx \exp \left( {\ln {\alpha ^\alpha } - \alpha  - \frac{{{\delta ^2}}}{{2\alpha }}} \right) = \exp \left( {\ln {\alpha ^\alpha }} \right).\exp \left( { - \alpha } \right).\exp \left( { - \frac{{{\delta ^2}}}{{2\alpha }}} \right)\]

\[ = {\alpha ^\alpha }.{e^{ - \alpha }}.\exp \left( { - \frac{{{\delta ^2}}}{{2\alpha }}} \right) = {\left( {\frac{\alpha }{e}} \right)^\alpha }.\exp \left( { - \frac{{{\delta ^2}}}{{2\alpha }}} \right)\]

Thay vào biểu thức dưới dấu tích phân trong hàm Gamma, ta được:

\[\alpha ! = \int\limits_0^{ + \infty } {{{\left( {\frac{\alpha }{e}} \right)}^\alpha }.\exp \left( { - \frac{{{\delta ^2}}}{{2\alpha }}} \right)d\left( {\alpha  + \delta } \right)}  = {\left( {\frac{\alpha }{e}} \right)^\alpha }\int\limits_0^{ + \infty } {\exp \left( { - \frac{{{\delta ^2}}}{{2\alpha }}} \right)d\left( \delta  \right)}  = {\left( {\frac{\alpha }{e}} \right)^\alpha }.I\]

Nhận thấy bây giờ, chúng ta phải giải quyết cái tích phân sau:

\[I = \int\limits_0^{ + \infty } {\exp \left( { - \frac{{{\delta ^2}}}{{2\alpha }}} \right)d\left( \delta  \right)}  = \int\limits_0^{ + \infty } {{e^{\frac{{ - {\delta ^2}}}{{2\alpha }}}}d\left( \delta  \right)} \]

Tính tích phân này ko khó, nhưng tránh để lặp lại trong chuỗi bài viết (gõ công thức toán bằng Latex lâu vãi lúa), nên tôi sẽ trình bày cách tính tích phân này trong lúc nói về phân phối Gaussian ở bài viết tiếp theo. Còn bây giờ, chúng ta chỉ cần biết tích phân trên có giá trị là $I = \sqrt {2\pi \alpha }$ là đủ để xấp xỉ Binomial về Gaussian rồi.

Từ tất cả các biến đổi trên, chúng ta thu được kết quả của phép xấp xỉ Stirling:

\[\alpha ! = {\left( {\frac{\alpha }{e}} \right)^\alpha }\sqrt {2\pi \alpha } \]

Rồi, bây giờ bắt đầu vào tiết mục chính của bài viết này này. Chúng ta bắt đầu khai phá công thức của phân phối Binomial và đưa nó về công thức dưới dạng phân phối Gaussian. Lưu ý rằng các biến đổi sau đây, nhìn qua thì cứ tưởng phải dùng nhiều kiến thức lằng nhằng, nhưng thật ra chỉ cần dùng 1 chút kiến thức Giải tích là bạn có thể hiểu được rồi! Với mục đích xấp xỉ:

\[C_n^k.{p^x}.{q^{n - x}} \approx \frac{1}{{\sqrt {2\pi npq} }}\exp \left[ { - \frac{{{{\left( {x - np} \right)}^2}}}{{2npq}}} \right]\]

Chúng ta sẽ biến đổi từ vế trái qua vế phải như sau.

\[Bin\left( {x|n,p} \right) = \left( \begin{array}{l} n\\ x \end{array} \right){p^x}{\left( {1 - p} \right)^{n - x}} = C_n^x.{p^x}{\left( {1 - p} \right)^{n - x}}\]

\[=\frac{{n!}}{{x!.\left( {n - x} \right)!}}.{p^x}{\left( {1 - p} \right)^{n - x}} = \frac{{\sqrt {2\pi n} {{\left( {\frac{n}{e}} \right)}^n}}}{{\sqrt {2\pi x} {{\left( {\frac{x}{e}} \right)}^x}.\sqrt {2\pi \left( {n - x} \right)} .{{\left( {\frac{{n - x}}{e}} \right)}^{n - x}}}}.{p^x}{\left( {1 - p} \right)^{n - x}}\]

\[ = \frac{{\sqrt {2\pi } }}{{\sqrt {2\pi } .\sqrt {2\pi } }}.\frac{{\sqrt n }}{{\sqrt x .\sqrt {n - x} }}.\frac{{{n^n}}}{{{x^x}.{{\left( {n - x} \right)}^{n - x}}}}.\frac{{{e^{ - n}}}}{{{e^{ - x}}.{e^{ - \left( {n - x} \right)}}}}.{p^x}{\left( {1 - p} \right)^{n - x}}\]

\[ = \frac{1}{{\sqrt {2\pi } }}.\frac{{{n^{n + \frac{1}{2}}}}}{{{x^{x + \frac{1}{2}}}.{{\left( {n - x} \right)}^{n - x + \frac{1}{2}}}}}.{p^x}{\left( {1 - p} \right)^{n - x}} = \frac{1}{{\sqrt {2\pi } .{n^{\frac{1}{2}}}}}.\frac{{{n^{n + \frac{1}{2}}}.{n^{\frac{1}{2}}}}}{{{x^{x + \frac{1}{2}}}.{{\left( {n - x} \right)}^{n - x + \frac{1}{2}}}}}.{p^x}{\left( {1 - p} \right)^{n - x}}\]

\[ = \frac{1}{{\sqrt {2\pi n} }}.\frac{{{n^{n + \frac{1}{2} + \frac{1}{2} + x - x}}}}{{{x^{x + \frac{1}{2}}}.{{\left( {n - x} \right)}^{n - x + \frac{1}{2}}}}}.{p^x}{\left( {1 - p} \right)^{n - x}} = \frac{1}{{\sqrt {2\pi n} }}.\frac{{{n^{\left( {x + \frac{1}{2}} \right) + \left( {n - x + \frac{1}{2}} \right)}}}}{{{x^{x + \frac{1}{2}}}.{{\left( {n - x} \right)}^{n - x + \frac{1}{2}}}}}.{p^x}{\left( {1 - p} \right)^{n - x}}\]

\[ = \frac{1}{{\sqrt {2\pi n} }}.{\left( {\frac{n}{x}} \right)^{x + \frac{1}{2}}}.{\left( {\frac{n}{{n - x}}} \right)^{n - x + \frac{1}{2}}}{p^x}{\left( {1 - p} \right)^{n - x}} = \frac{1}{{\sqrt {2\pi n} }}.{\left( {\frac{x}{n}} \right)^{ - x - \frac{1}{2}}}.{\left( {\frac{{n - x}}{n}} \right)^{ - n + x - \frac{1}{2}}}{p^x}{\left( {1 - p} \right)^{n - x}}\]

Đặt $x=np+\epsilon$, tiếp tục thay vào biến đổi:

\[ = \frac{1}{{\sqrt {2\pi n} }}.{\left( {\frac{{np + \varepsilon }}{n}} \right)^{ - x - \frac{1}{2}}}.{\left( {\frac{{n - np - \varepsilon }}{n}} \right)^{ - n + x - \frac{1}{2}}}{p^x}{\left( {1 - p} \right)^{n - x}} = \frac{1}{{\sqrt {2\pi n} }}.{\left( {p + \frac{\varepsilon }{n}} \right)^{ - x - \frac{1}{2}}}.{\left( {1 - p - \frac{\varepsilon }{n}} \right)^{ - n + x - \frac{1}{2}}}{p^x}{\left( {1 - p} \right)^{n - x}}\]

\[ = \frac{1}{{\sqrt {2\pi n} }}{\left[ {p\left( {1 + \frac{\varepsilon }{{np}}} \right)} \right]^{ - x - \frac{1}{2}}}.{\left[ {\left( {1 - p} \right)\left( {1 - \frac{\varepsilon }{{n\left( {1 - p} \right)}}} \right)} \right]^{ - n + x - \frac{1}{2}}}{p^x}{\left( {1 - p} \right)^{n - x}}\]

\[ = \frac{1}{{\sqrt {2\pi n} }}.{p^{ - x - \frac{1}{2}}}.{\left( {1 - p} \right)^{ - n + x - \frac{1}{2}}}.{\left( {1 + \frac{\varepsilon }{{np}}} \right)^{ - x - \frac{1}{2}}}.{\left( {1 - \frac{\varepsilon }{{n\left( {1 - p} \right)}}} \right)^{ - n + x - \frac{1}{2}}}.{p^x}{\left( {1 - p} \right)^{n - x}}\]

\[ = \frac{1}{{\sqrt {2\pi n} }}.{\left( {1 + \frac{\varepsilon }{{np}}} \right)^{ - x - \frac{1}{2}}}.{\left( {1 - \frac{\varepsilon }{{n\left( {1 - p} \right)}}} \right)^{ - n + x - \frac{1}{2}}}.{p^{ - \frac{1}{2}}}{\left( {1 - p} \right)^{ - \frac{1}{2}}}\]

\[ = \frac{1}{{\sqrt {2\pi np\left( {1 - p} \right)} }}.{\left( {1 + \frac{\varepsilon }{{np}}} \right)^{ - x - \frac{1}{2}}}.{\left( {1 - \frac{\varepsilon }{{n\left( {1 - p} \right)}}} \right)^{ - n + x - \frac{1}{2}}}\]

\[ = \frac{1}{{\sqrt {2\pi np\left( {1 - p} \right)} }}\exp \left\{ {\ln \left[ {{{\left( {1 + \frac{\varepsilon }{{np}}} \right)}^{ - x - \frac{1}{2}}}.{{\left( {1 - \frac{\varepsilon }{{n\left( {1 - p} \right)}}} \right)}^{ - n + x - \frac{1}{2}}}} \right]} \right\}\]

\[\frac{1}{{\sqrt {2\pi np\left( {1 - p} \right)} }}\exp \left\{ {\ln {{\left( {1 + \frac{\varepsilon }{{np}}} \right)}^{ - x - \frac{1}{2}}} + \ln {{\left( {1 - \frac{\varepsilon }{{n\left( {1 - p} \right)}}} \right)}^{ - n + x - \frac{1}{2}}}} \right\}\]

\[ = \frac{1}{{\sqrt {2\pi np\left( {1 - p} \right)} }}\exp \left[ {\left( { - x - \frac{1}{2}} \right)\ln \left( {1 + \frac{\varepsilon }{{np}}} \right) + \left( { - n + x - \frac{1}{2}} \right)\ln \left( {1 - \frac{\varepsilon }{{n\left( {1 - p} \right)}}} \right)} \right]\]

\[ = \frac{1}{{\sqrt {2\pi np\left( {1 - p} \right)} }}\exp \left[ {\left( { - np - \varepsilon  - \frac{1}{2}} \right)\ln \left( {1 + \frac{\varepsilon }{{np}}} \right) + \left( { - n + np + \varepsilon  - \frac{1}{2}} \right)\ln \left( {1 - \frac{\varepsilon }{{n\left( {1 - p} \right)}}} \right)} \right]\]

\[ = \frac{1}{{\sqrt {2\pi np\left( {1 - p} \right)} }}\exp \left[ {\left( { - np - \varepsilon  - \frac{1}{2}} \right)\ln \left( {1 + \frac{\varepsilon }{{np}}} \right) + \left( { - n\left( {1 - p} \right) + \varepsilon  - \frac{1}{2}} \right)\ln \left( {1 - \frac{\varepsilon }{{n\left( {1 - p} \right)}}} \right)} \right]\]

Xét khai triển Maclaurin của hàm số $f(x)=ln(x+1)$ ta có:

\[f\left( x \right) = \ln \left( {1 + x} \right) \approx x - \frac{{{x^2}}}{2} + ... \Rightarrow f\left( { - x} \right) = \ln \left( {1 - x} \right) \approx  - x - \frac{{{x^2}}}{2}\]

Thực hiện khai triển Maclaurin trên cho các thừa số logarit Napier, ta được:

\[\ln \left( {1 + \frac{\varepsilon }{{np}}} \right) \approx \frac{\varepsilon }{{np}} - \frac{1}{2}.{\left( {\frac{\varepsilon }{{np}}} \right)^2}\]

\[\ln \left( {1 - \frac{\varepsilon }{{n\left( {1 - p} \right)}}} \right) \approx \frac{\varepsilon }{{n\left( {1 - p} \right)}} - \frac{1}{2}.{\left( {\frac{\varepsilon }{{n\left( {1 - p} \right)}}} \right)^2}\]

Ốp vào biến đổi của Binomial và tiếp tục biến đổi, ta được:

\[Bin\left( {x|np} \right) = \frac{1}{{\sqrt {2\pi np\left( {1 - p} \right)} }}\exp \left[ {\left( { - np - \varepsilon  - \frac{1}{2}} \right)\left[ {\frac{\varepsilon }{{np}} - \frac{1}{2}.{{\left( {\frac{\varepsilon }{{np}}} \right)}^2}} \right] + \left( { - n\left( {1 - p} \right) + \varepsilon  - \frac{1}{2}} \right)\left[ {\frac{\varepsilon }{{n\left( {1 - p} \right)}} - \frac{1}{2}.{{\left( {\frac{\varepsilon }{{n\left( {1 - p} \right)}}} \right)}^2}} \right]} \right]\]

(Đoạn này dài quá mình ngại gõ lại lên đây, nên viết luôn kết quả rút gọn, chỉ việc nhân tung ra thôi! @@)

\[ = \frac{1}{{\sqrt {2\pi np\left( {1 - p} \right)} }}\exp \left[ { - \varepsilon  + \frac{{{\varepsilon ^2}}}{{2np}} - \frac{{{\varepsilon ^2}}}{{np}} + \varepsilon  + \frac{{{\varepsilon ^2}}}{{2n\left( {1 - p} \right)}} - \frac{{{\varepsilon ^2}}}{{n\left( {1 - p} \right)}}} \right]\]

\[ = \frac{1}{{\sqrt {2\pi np\left( {1 - p} \right)} }}\exp \left[ {\frac{{ - {\varepsilon ^2}}}{{2np}} + \frac{{ - \varepsilon }}{{2n\left( {1 - p} \right)}}} \right] = \frac{1}{{\sqrt {2\pi np\left( {1 - p} \right)} }}\exp \left[ {\frac{{ - {\varepsilon ^2}}}{{2np\left( {1 - p} \right)}}} \right]\]

Móa, tốt rồi. Đến đây chắc hẳn là bạn cũng đã thấy hình dạng của phân phối Gaussian! Nếu bạn chưa thấy, hãy nhớ lại bên trên ta đã đổi biến $x=np+\epsilon$, bây giờ ta chỉ việc đưa về biến ban đầu. Coi như 1 chút bài tập tự luyện ngắn.

Tóm lại.

Suốt từ đầu bài đến giờ, chúng ta đã xấp xỉ phân phối Binomial về 2 phân phối tổng quát hơn là Poisson và Gaussian. Tóm lại, khi số lần thực hiện phép thử tung đồng xu tiến ra vô cực:

• Nếu xác suất thành công $\theta$ là đủ nhỏ sao cho $\lambda=n\theta$ là 1 số hữu hạn, phân phối Binomial sẽ xấp xỉ về phân phối Poisson. Lúc này, ta sẽ ko quan tâm xác suất thành công của từng phép thử đơn lẻ, mà sẽ quan tâm đến tham số $\lambda$ đại diện cho tần suất thành công trong 1 đơn vị thời gian cố định.
• Tổng quát hơn, nếu xác suất thành công $\theta$ ko đủ nhỏ để $\lambda=n\theta$ là 1 số hữu hạn, khi đó phân phối Binomial sẽ xấp xỉ về phân phối Gaussian. Cũng phải lưu ý thêm, Gaussian là phân phối mô tả cho biến ngẫu nhiên liên tục 1 chiều, nên khi số phép thử là quá lớn, ta mới có thể thực hiện phép xấp xỉ này.

Kể ra thì hầu hết các biến đổi trên đều ko có j là khó hiểu lắm, chỉ đơn thuần là kiến thức THPT kết hợp thêm 1 chút kiến thức của Toán cao cấp trên đại học thôi. Ban đầu khi tôi tìm hiểu, các bài viết hầu như biến đổi khá vắn tắt, có lẽ là dành cho các bạn nào được A, A+ các môn Toán cao cấp thì sẽ hiểu ngay được. Nếu ko đặt bút nháp theo cách họ biến đổi, mà cứ đọc liếng thoắng cho qua, tôi khó có thể cảm nhận được sự vắn tắt làm thiếu thỏa mãn đó. Do vậy, tôi cũng đã đọc thêm và biến đổi lại chi tiết hơn với mong muốn gỡ rối hầu hết mọi sự nghi ngờ của bản thân; ngoài ra cũng giúp bản thân hiểu thêm hơn về ý đồ của lời giải và cách biến đổi.

Seri bài viết này tưởng nhanh mà có vẻ phải kéo dài khá nhiều. Mỗi lần viết bài, gõ công thức toán Latex thế này cũng tốn khá nhiều thời gian so với việc chỉ ngồi kể chuyện và xạo chó. Chúng ta còn cần xấp xỉ Poisson về Gaussian, sử dụng Beta để xấp xỉ Binomial, sử dụng Dirichlet để xấp xỉ Multinomial, suy rộng Beta thành Dirichlet, cách mà có thể xấp xỉ lẫn nhau giữa Beta vs Gaussian 1 chiều và Dirichlet vs Gaussian nhiều chiều. Ngoài ra còn phân phối Student - phân phối thông dụng nhất thế giới - cũng liên quan đến phân phối Gaussian chuẩn tắc và phân phối Chi-square (phân phối khi - bình phương).