Quan hệ giữa các phân phối xác suất thông dụng nhất: Gaussian là giới hạn cuối cùng.
Trong bài viết trước, tôi đã trình bày về việc xấp xỉ Binomial về Poisson (khi xác suất thành công rất hiếm) và về Gaussian (khi xác suất thành công ko hề hiếm). Việc chứng minh về căn bản cũng ko dùng nhiều kiến thức Toán cao cấp lắm, hầu như vẫn chỉ cần dùng kiến thức Toán ở bậc THPT là có thể hiểu được (mệt cái là gõ Latex hơi lắm thôi).
Tiếp tục seri bài viết, trong bài viết này, tôi sẽ tiếp tục tổng quát hóa phân phối Poisson về Gaussian. Khi đã tới được Gaussian rồi, một loạt các phân phối xác suất mới sẽ xuất hiện theo, vì chúng đều xuất phát từ việc lấy mẫu dựa trên Gaussian.
Poisson sẽ tiến về Gaussian.
Nếu đi từ Binomial, khi $\lambda=n.\theta$ tiến đến vô hạn, Binomial sẽ tiến về Gaussian. Tuy nhiên, nếu ko đi từ Binomial, mà đi từ Poisson thì sao. Sẽ ra sao khi $\lambda$ của Poisson tiến đến $+\infty$? Ừ thì có thể coi rằng khi $\lambda\to+\infty$, đồng nghĩa với việc $n\to+\infty$ (vì $\theta\le1$ bị giới hạn; nếu như $\theta$ không quá nhỏ (hoặc ko quá lớn), thì việc Poisson tiến về Gaussian có thể quy về việc Binomial tiến về Gaussian; vì lúc này, Poisson chính là Binomial.
Thế nhưng, nếu $\theta$ lại quá nhỏ thì sao, lúc này Binomial tiến về Poisson chứ ko phải về Gaussian, vậy ta chỉ còn cách chứng minh trực tiếp Poisson cuối cùng cũng sẽ phải tiến về Gaussian thôi!
Thật ra thì nếu sử dụng kết quả của Định lý giới hạn trung tâm, ta hoàn toàn có thể khẳng định Poisson sẽ tiến về Gaussian! Nhưng nếu nói toẹt ra như vậy thì mất hay; vs lại việc chứng minh Định lý giới hạn trung tâm cũng vướng phải khái niệm Moment Generate Function (Hàm sinh momen). Mà nếu đã dùng khái niệm này, thì việc chứng minh Poisson sẽ xấp xỉ về Gaussian còn đỡ đao to búa lớn hơn là đi chứng minh Định lý giới hạn trung tâm. Do đó trong giới hạn của chuỗi bài viết này, tôi sẽ trình bày cách chứng minh trực tiếp một cách thủ công, thay vì sử dụng qua các khái niệm nâng cao.
Như ta đã biết, hàm mật độ (khối) xác suất của phân phối Poisson có dạng:
\[Po(x|\lambda)=e^{-\lambda}.\frac{\lambda^x}{x!}\]
Với $\lambda$ là kỳ vọng, cũng đồng thời là phương sai; biểu thị tần suất thành công của phép thử trong 1 đơn vị thời gian. Khi học Xác suất thống kê, bạn sẽ được dạy rằng "khi $\lambda\ge20$, có thể xấp xỉ Poisson về Gaussian". Ý của câu nhận xét này nghĩa là: "khi $\lambda\to+\infty$, Poisson sẽ tiến về Gausian". Để chứng minh điều này, trước tiên ta phải hiểu, điều j sẽ xảy ra khi mà $\lambda\to+\infty$? $\lambda$ biểu thị tần suất thành công của phép thử trong 1 đơn vị thời gian. Thế nên khi $\lambda\to+\infty$, nghĩa là tần suất thành công của phép thử là rất lớn. $\lambda$ càng lớn, đồng nghĩa với việc cứ tung đồng xu lần nào là gần như sẽ ngửa lần đó (nếu ta cần khảo sát mặt ngửa). Vậy nên, nếu ta kéo dãn đơn vị thời gian ra thành $+\infty$, thì lúc này, $\lambda\approx n$.
Do vậy, đặt $x=\lambda(1+\delta)$, với $\delta\ll1$, lúc này $\lambda\gg1$. Sử dụng lại xấp xỉ Stirling trong bài hôm trước cho $n!$, ta được: $x!\approx\sqrt{2\pi x}.e^{-x}x^x$. Thay vào hàm mật độ của phân phối Poisson, ta thu được:
\[\mathop {\lim }\limits_{^{\lambda\to+\infty}_{x\to+\infty}} Po\left( {x|\lambda } \right) =\mathop {\lim }\limits_{^{\lambda\to+\infty}_{\delta\to0}} \frac{{{e^{ - \lambda }}.{\lambda ^{\lambda \left( {1 + \delta } \right)}}}}{{\sqrt {2\pi .\lambda \left( {1 + \delta } \right)} .{e^{ - \lambda \left( {1 + \delta } \right)}}.{{\left[ {\lambda \left( {1 + \delta } \right)} \right]}^{\lambda \left( {1 + \delta } \right)}}}} =\mathop {\lim }\limits_{^{\lambda\to+\infty}_{\delta\to0}} \frac{{{e^{\lambda \delta }}.{{\left( {1 + \delta } \right)}^{ - \left[ {\lambda \left( {1 + \delta } \right) + \frac{1}{2}} \right]}}}}{{\sqrt {2\pi \lambda } }}\]
\[\Leftrightarrow ln\left[\mathop {\lim }\limits_{^{\lambda\to+\infty}_{x\to+\infty}} Po\left( {x|\lambda } \right)\right]=ln\left\{\mathop {\lim }\limits_{^{\lambda\to+\infty}_{\delta\to0}} \frac{{{e^{\lambda \delta }}.{{\left( {1 + \delta } \right)}^{ - \left[ {\lambda \left( {1 + \delta } \right) + \frac{1}{2}} \right]}}}}{{\sqrt {2\pi \lambda } }}\right\}=\mathop {\lim }\limits_{^{\lambda\to+\infty}_{\delta\to0}}\left\{{\ln \left( {\frac{{{e^{\lambda \delta }}}}{{\sqrt {2\pi \lambda } }}} \right) + \ln {{\left( {1 + \delta } \right)}^{ - \left[ {\lambda \left( {1 + \delta } \right) + \frac{1}{2}} \right]}}}\right\}\]
\[=\mathop {\lim }\limits_{^{\lambda\to+\infty}_{x\to+\infty}} \left\{ {\ln \left( {\frac{{{e^{\lambda \delta }}}}{{\sqrt {2\pi \lambda } }}} \right) - \left[ {\lambda \left( {1 + \delta } \right) + \frac{1}{2}} \right]\ln \left( {1 + \delta } \right)} \right\}\]
Theo khai triển Maclaurin với $\delta\to0$ vô cùng bé, ta có xấp xỉ $ln(1+\delta)=\delta - \frac{{{\delta ^2}}}{2} + {\rm O}\left( {{\delta ^3}} \right)$, tiếp tục biến đổi, ta được:
\[=\mathop {\lim }\limits_{^{\lambda\to+\infty}_{x\to+\infty}} \left\{ {\ln \left( {\frac{{{e^{\lambda \delta }}}}{{\sqrt {2\pi \lambda } }}} \right) - \left(\lambda + \lambda \delta + \frac{1}{2} \right)\left[ {\delta - \frac{{{\delta ^2}}}{2} + {\rm O}\left( {{\delta ^3}} \right)} \right]} \right\}\]
\[=\mathop {\lim }\limits_{^{\lambda\to+\infty}_{x\to+\infty}} \left[ {\ln \left( {\frac{{{e^{\lambda \delta }}}}{{\sqrt {2\pi \lambda } }}} \right) - \left( {\lambda \delta + \frac{{\lambda {\delta ^2}}}{2} + {\rm O}\left( \delta^3 \right)} \right)} \right]\]
\[\Leftrightarrow \mathop {\lim }\limits_{^{\lambda\to+\infty}_{x\to+\infty}} Po\left( {x|\lambda } \right)=\mathop {\lim }\limits_{^{\lambda\to+\infty}_{\delta\to0}}\frac{{{e^{\lambda \delta }}.{e^{ - \lambda \delta - \frac{{\lambda {\delta ^2}}}{2}}}}}{{\sqrt {2\pi \lambda } }}=\mathop {\lim }\limits_{^{\lambda\to+\infty}_{\delta\to0}}\frac{{{e^{ - \frac{{\lambda {\delta ^2}}}{2}}}}}{{\sqrt {2\pi \lambda } }}\]
Bây giờ, thế ngược lại các biến về $x$. Vì lúc đầu, ta đặt $x=\lambda(1+\delta)$, nên ta thay $\delta=\frac{x-\lambda}{\lambda}$ vào giới hạn đang biến đổi, ta sẽ được: $\mathop {\lim }\limits_{^{\lambda\to+\infty}_{x\to+\infty}} Po\left( {x|\lambda } \right)=\frac{1}{{\sqrt {2\pi \lambda } }}{e^{ - \frac{{{{\left( {x - \lambda } \right)}^2}}}{{2\lambda }}}}$
\[=\mathop {\lim }\limits_{^{\lambda\to+\infty}_{x\to+\infty}} \left\{ {\ln \left( {\frac{{{e^{\lambda \delta }}}}{{\sqrt {2\pi \lambda } }}} \right) - \left[ {\lambda \left( {1 + \delta } \right) + \frac{1}{2}} \right]\ln \left( {1 + \delta } \right)} \right\}\]
Theo khai triển Maclaurin với $\delta\to0$ vô cùng bé, ta có xấp xỉ $ln(1+\delta)=\delta - \frac{{{\delta ^2}}}{2} + {\rm O}\left( {{\delta ^3}} \right)$, tiếp tục biến đổi, ta được:
\[=\mathop {\lim }\limits_{^{\lambda\to+\infty}_{x\to+\infty}} \left\{ {\ln \left( {\frac{{{e^{\lambda \delta }}}}{{\sqrt {2\pi \lambda } }}} \right) - \left(\lambda + \lambda \delta + \frac{1}{2} \right)\left[ {\delta - \frac{{{\delta ^2}}}{2} + {\rm O}\left( {{\delta ^3}} \right)} \right]} \right\}\]
\[=\mathop {\lim }\limits_{^{\lambda\to+\infty}_{x\to+\infty}} \left[ {\ln \left( {\frac{{{e^{\lambda \delta }}}}{{\sqrt {2\pi \lambda } }}} \right) - \left( {\lambda \delta + \frac{{\lambda {\delta ^2}}}{2} + {\rm O}\left( \delta^3 \right)} \right)} \right]\]
\[\Leftrightarrow \mathop {\lim }\limits_{^{\lambda\to+\infty}_{x\to+\infty}} Po\left( {x|\lambda } \right)=\mathop {\lim }\limits_{^{\lambda\to+\infty}_{\delta\to0}}\frac{{{e^{\lambda \delta }}.{e^{ - \lambda \delta - \frac{{\lambda {\delta ^2}}}{2}}}}}{{\sqrt {2\pi \lambda } }}=\mathop {\lim }\limits_{^{\lambda\to+\infty}_{\delta\to0}}\frac{{{e^{ - \frac{{\lambda {\delta ^2}}}{2}}}}}{{\sqrt {2\pi \lambda } }}\]
Bây giờ, thế ngược lại các biến về $x$. Vì lúc đầu, ta đặt $x=\lambda(1+\delta)$, nên ta thay $\delta=\frac{x-\lambda}{\lambda}$ vào giới hạn đang biến đổi, ta sẽ được: $\mathop {\lim }\limits_{^{\lambda\to+\infty}_{x\to+\infty}} Po\left( {x|\lambda } \right)=\frac{1}{{\sqrt {2\pi \lambda } }}{e^{ - \frac{{{{\left( {x - \lambda } \right)}^2}}}{{2\lambda }}}}$
Đây chính là phân phối Gaussian với độ lệch chuẩn $\mu=\lambda$ và phương sai $\sigma^2=\lambda$.
Phân phối Gaussian.
Phân phối Gaussian - hay còn gọi là phân phối Chuẩn - là phân phối xác suất thông dụng nhất, được bắt gặp nhiều nhất trong thực tế. Định lý giới hạn trung tâm đã khẳng định việc lấy mẫu của rất nhiều các biến ngẫu nhiên theo cùng 1 phân phối bất kỳ thì sẽ cho phân phối xác suất tổng có kết quả tuân theo phân phối Gaussian. Như ta đã biết, Gaussian là phân phối xác suất của biến ngẫu nhiên liên tục có kỳ vọng $\mu$ và phương sai $\sigma^2$; khi đó, công thức hàm mật độ xác suất của Gaussian sẽ là:
\[f\left(x|\mu,\sigma^2\right)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{\left(x-\mu\right)^2}{2\sigma^2}}=\frac{1}{\sqrt{2\pi\sigma^2}}exp\left[-\frac{\left(x-\mu\right)^2}{2\sigma^2}\right]\]
Hàm phân phối xác suất của biến ngẫu nhiên liên tục đều có 2 thành phần: KERNEL (hạt nhân) và NORNAMLIZING CONSTANT (hằng số chuẩn hóa - NormConst). Trong đó, quan trọng nhất là Kernel; còn NormConst chẳng qua chỉ là hằng số được nhân thêm vào để đảm bảo tích phân của Kernel trên toàn miền xác định của biến ngẫu nhiên liên tục đó phải có giá trị bằng 1, tức là hàm tích lũy xác suất trên toàn miền phải bằng 1.
Ví dụ với phân phối Gaussian bên trên, Kernel chính là $exp\left[-\frac{\left(x-\mu\right)^2}{2\sigma^2}\right]$, còn NormConst chính là $\frac{1}{\sqrt{2\pi\sigma^2}}$.
Giả sử chưa biết NormConst, ta phải đi tìm NormConst để Kernel này thỏa mãn tính chất $\int\limits_{ - \infty }^{ + \infty } {f(x)dx} = 1$. Mà $f(x)=NormConst.Kernel$, nên ta thấy rằng:
\[1=\int\limits_{-\infty}^{+\infty}{f(x)dx}=\int\limits_{-\infty}^{+\infty} NormConst.Kernel = NormConst.\int\limits_{ - \infty }^{ + \infty }Kernel \]
Thế nên, ta được kết quả:
\[NormConst =\frac{1}{\int\limits_{ - \infty }^{ + \infty }Kernel} \]
Vậy nên, trong trường hợp Gaussian, ta có thể tìm ra NormConst bằng việc tính biểu thức:
\[NormConst =\frac{1}{\int\limits_{ - \infty }^{ + \infty }exp\left[-\frac{\left(x-\mu\right)^2}{2\sigma^2}\right]dx} = \frac{1}{I} \]
Trong bài viết trước, ở quá trình chứng minh Ước lượng Stirling, tôi đã từng nói đến 1 dạng cụ thể của tích phân này rồi; và trong bài này, ta gặp phải tích phân tổng quát hơn. Tích phân I dưới mẫu số của biểu thức kia cũng ko khó tính lắm; tuy nhiên để tính được thì phải sử dụng qua phép biến đổi hệ tọa độ trong Giải tích 1 của Toán cao cấp. Cụ thể ta sẽ biến đổi sang hệ tọa độ cực để tính tích phân này.
Đơn giản thôi, đầu tiên, ta sẽ co về dạng "chuẩn tắc", chính là dạng trong bài viết trước. Cụ thể, đặt $u=\frac{x-\mu}{\sigma}\Rightarrow dx=\sigma du$, thay vào tích phân $I$, ta được:
\[I = \int\limits_{ - \infty }^{ + \infty } {exp\left[ { - \frac{{{{\left( {x - \mu } \right)}^2}}}{{2{\sigma ^2}}}} \right]dx} = \sigma \int\limits_{ - \infty }^{ + \infty } {exp\left( { - \frac{{{u^2}}}{2}} \right)du} \]
\[ \Rightarrow {I^2} = \left[ {\sigma \int\limits_{ - \infty }^{ + \infty } {exp\left( { - \frac{{{u^2}}}{2}} \right)du} } \right]\left[ {\sigma \int\limits_{ - \infty }^{ + \infty } {exp\left( { - \frac{{{u^2}}}{2}} \right)du} } \right]\]
\[ = \left[ {\sigma \int\limits_{ - \infty }^{ + \infty } {exp\left( { - \frac{{{u^2}}}{2}} \right)du} } \right]\left[ {\sigma \int\limits_{ - \infty }^{ + \infty } {exp\left( { - \frac{{{v^2}}}{2}} \right)dv} } \right] = {\sigma ^2}\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\exp \left( { - \frac{{{u^2} + {v^2}}}{2}} \right)du} dv}\]
Tiếp theo, ta chuyển về hệ tọa độ cực thông qua phép đặt:
\[\left\{ \begin{array}{l} u = r\cos \theta \\ v = r\sin \theta \end{array} \right. \Rightarrow \left[ \begin{array}{l} du\\ dv \end{array} \right] = \left[ \begin{array}{l} \begin{array}{*{20}{c}} {\frac{{\partial u}}{{\partial r}}}&{\frac{{\partial u}}{{\partial \theta }}} \end{array}\\ \begin{array}{*{20}{c}} {\frac{{\partial v}}{{\partial r}}}&{\frac{{\partial v}}{{\partial \theta }}} \end{array} \end{array} \right]\left[ \begin{array}{l} dr\\ d\theta \end{array} \right] = \left[ \begin{array}{l} \begin{array}{*{20}{c}} {\cos \theta }&{ - r\sin \theta } \end{array}\\ \begin{array}{*{20}{c}} {\sin \theta }&{r\cos \theta } \end{array} \end{array} \right]\left[ \begin{array}{l} dr\\ d\theta \end{array} \right]\]
\[ \Rightarrow du.dv = \left| \begin{array}{l} \begin{array}{*{20}{c}} {\cos \theta }&{ - r\sin \theta } \end{array}\\ \begin{array}{*{20}{c}} {\sin \theta }&{r\cos \theta } \end{array} \end{array} \right|dr.d\theta = r.dr.d\theta \]
Thực hiện đổi cận và thay vào tích phân, ta được:
\[{I^2} = {\sigma ^2}\int\limits_0^{ + \infty } {\left[ {\int\limits_0^{2\pi } {r.{{\mathop{\rm e}\nolimits} ^{ - \frac{{{r^2}}}{2}}}.d\theta } } \right]dr} = {\sigma ^2}\int\limits_0^{ + \infty } {2\pi r{{\mathop{\rm e}\nolimits} ^{ - \frac{{{r^2}}}{2}}}dr} = 2\pi {\sigma ^2}\]
Do đó, ta thu được kết quả $I=\sqrt{2\pi\sigma^2}$. Vậy $NormConst = \frac{1}{I}=\frac{1}{\sqrt{2\pi\sigma^2}}$
Hàm mật độ xác suất của mọi phân phối xác suất của biến ngẫu nhiên liên tục đều có đặc tính này. Hằng số chuẩn hóa chỉ là hình thức, quan trọng nhất vẫn là Kernel của hàm mật độ. Có những lúc, ko biết được NormConst, nhưng chúng ta vẫn có thể lấy mẫu được theo Kernel được mà ko cần tính toán rõ ràng NormConst có giá trị là bao nhiêu! Đúng vậy, phương pháp lấy mẫu tôi nói đến ở đây chính là phương pháp Markov chain Monte Carlo (cũng có thể là Monte Carlo Markov chain) - hay MCMC. Đây là phương pháp lấy mẫu rất mạnh, đến mức ta chỉ cần biết Kernel! Nhưng đây lại là 1 câu chuyện hay ho khác, và sẽ được viết ở những bài viết sau.
Phân phối Gaussian đương nhiên cũng có dạng tổng quát cho biến ngẫu nhiên nhiều chiều. Điểm khác biệt ở đây chính là ma trận hiệp phương sai. Tuy nhiên tôi sẽ ko đi vào cụ thể, vì sách Xác suất thống kê nói cái này nhiều rồi.
\[X\sim Norm(\mu=0,\sigma^2=1)=f(x|\mu=0,\sigma^2=1)=\frac{1}{\sqrt{2\pi}}exp\left(-\frac{x^2}{2}\right) \]
Các phân phối sau đây đều có các giai đoạn thành phần được lấy mẫu từ phân phối chuẩn tắc. Thật ra thì tôi mới chỉ nghiên cứu về Machine Learning nhiều thôi chứ Data Analysis thì chưa nhiều, nên mấy cái phân phối về sau, tôi chỉ trình bày ra thôi, chứ cũng chưa sử dụng để làm j bao giờ cả.
Trong bài viết trước, ở quá trình chứng minh Ước lượng Stirling, tôi đã từng nói đến 1 dạng cụ thể của tích phân này rồi; và trong bài này, ta gặp phải tích phân tổng quát hơn. Tích phân I dưới mẫu số của biểu thức kia cũng ko khó tính lắm; tuy nhiên để tính được thì phải sử dụng qua phép biến đổi hệ tọa độ trong Giải tích 1 của Toán cao cấp. Cụ thể ta sẽ biến đổi sang hệ tọa độ cực để tính tích phân này.
Đơn giản thôi, đầu tiên, ta sẽ co về dạng "chuẩn tắc", chính là dạng trong bài viết trước. Cụ thể, đặt $u=\frac{x-\mu}{\sigma}\Rightarrow dx=\sigma du$, thay vào tích phân $I$, ta được:
\[I = \int\limits_{ - \infty }^{ + \infty } {exp\left[ { - \frac{{{{\left( {x - \mu } \right)}^2}}}{{2{\sigma ^2}}}} \right]dx} = \sigma \int\limits_{ - \infty }^{ + \infty } {exp\left( { - \frac{{{u^2}}}{2}} \right)du} \]
\[ \Rightarrow {I^2} = \left[ {\sigma \int\limits_{ - \infty }^{ + \infty } {exp\left( { - \frac{{{u^2}}}{2}} \right)du} } \right]\left[ {\sigma \int\limits_{ - \infty }^{ + \infty } {exp\left( { - \frac{{{u^2}}}{2}} \right)du} } \right]\]
\[ = \left[ {\sigma \int\limits_{ - \infty }^{ + \infty } {exp\left( { - \frac{{{u^2}}}{2}} \right)du} } \right]\left[ {\sigma \int\limits_{ - \infty }^{ + \infty } {exp\left( { - \frac{{{v^2}}}{2}} \right)dv} } \right] = {\sigma ^2}\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\exp \left( { - \frac{{{u^2} + {v^2}}}{2}} \right)du} dv}\]
Tiếp theo, ta chuyển về hệ tọa độ cực thông qua phép đặt:
\[\left\{ \begin{array}{l} u = r\cos \theta \\ v = r\sin \theta \end{array} \right. \Rightarrow \left[ \begin{array}{l} du\\ dv \end{array} \right] = \left[ \begin{array}{l} \begin{array}{*{20}{c}} {\frac{{\partial u}}{{\partial r}}}&{\frac{{\partial u}}{{\partial \theta }}} \end{array}\\ \begin{array}{*{20}{c}} {\frac{{\partial v}}{{\partial r}}}&{\frac{{\partial v}}{{\partial \theta }}} \end{array} \end{array} \right]\left[ \begin{array}{l} dr\\ d\theta \end{array} \right] = \left[ \begin{array}{l} \begin{array}{*{20}{c}} {\cos \theta }&{ - r\sin \theta } \end{array}\\ \begin{array}{*{20}{c}} {\sin \theta }&{r\cos \theta } \end{array} \end{array} \right]\left[ \begin{array}{l} dr\\ d\theta \end{array} \right]\]
\[ \Rightarrow du.dv = \left| \begin{array}{l} \begin{array}{*{20}{c}} {\cos \theta }&{ - r\sin \theta } \end{array}\\ \begin{array}{*{20}{c}} {\sin \theta }&{r\cos \theta } \end{array} \end{array} \right|dr.d\theta = r.dr.d\theta \]
Thực hiện đổi cận và thay vào tích phân, ta được:
\[{I^2} = {\sigma ^2}\int\limits_0^{ + \infty } {\left[ {\int\limits_0^{2\pi } {r.{{\mathop{\rm e}\nolimits} ^{ - \frac{{{r^2}}}{2}}}.d\theta } } \right]dr} = {\sigma ^2}\int\limits_0^{ + \infty } {2\pi r{{\mathop{\rm e}\nolimits} ^{ - \frac{{{r^2}}}{2}}}dr} = 2\pi {\sigma ^2}\]
Do đó, ta thu được kết quả $I=\sqrt{2\pi\sigma^2}$. Vậy $NormConst = \frac{1}{I}=\frac{1}{\sqrt{2\pi\sigma^2}}$
Hàm mật độ xác suất của mọi phân phối xác suất của biến ngẫu nhiên liên tục đều có đặc tính này. Hằng số chuẩn hóa chỉ là hình thức, quan trọng nhất vẫn là Kernel của hàm mật độ. Có những lúc, ko biết được NormConst, nhưng chúng ta vẫn có thể lấy mẫu được theo Kernel được mà ko cần tính toán rõ ràng NormConst có giá trị là bao nhiêu! Đúng vậy, phương pháp lấy mẫu tôi nói đến ở đây chính là phương pháp Markov chain Monte Carlo (cũng có thể là Monte Carlo Markov chain) - hay MCMC. Đây là phương pháp lấy mẫu rất mạnh, đến mức ta chỉ cần biết Kernel! Nhưng đây lại là 1 câu chuyện hay ho khác, và sẽ được viết ở những bài viết sau.
Phân phối Gaussian đương nhiên cũng có dạng tổng quát cho biến ngẫu nhiên nhiều chiều. Điểm khác biệt ở đây chính là ma trận hiệp phương sai. Tuy nhiên tôi sẽ ko đi vào cụ thể, vì sách Xác suất thống kê nói cái này nhiều rồi.
Anh em của phân phối Gaussian.
Khi đã đạt đến Gaussian, chúng ta sẽ mở ra 1 loạt các phân phối khác. Đầu tiên, nếu co các tham số của Gaussian về dạng chuẩn tắc - tức là $\mu=0$ và $\sigma^2=1$, ta sẽ thu được phân phối chuẩn tắc:\[X\sim Norm(\mu=0,\sigma^2=1)=f(x|\mu=0,\sigma^2=1)=\frac{1}{\sqrt{2\pi}}exp\left(-\frac{x^2}{2}\right) \]
Các phân phối sau đây đều có các giai đoạn thành phần được lấy mẫu từ phân phối chuẩn tắc. Thật ra thì tôi mới chỉ nghiên cứu về Machine Learning nhiều thôi chứ Data Analysis thì chưa nhiều, nên mấy cái phân phối về sau, tôi chỉ trình bày ra thôi, chứ cũng chưa sử dụng để làm j bao giờ cả.
Phân phối ${\chi ^2}$.
Có lẽ đây là phân phối xác suất có cách đọc tên hack não nhất. Lúc học Xác suất thống kê trên trường, chúng tôi đọc là "phân phối khi bình phương"; nhưng ký tự $\chi$ kia thì lại được đọc theo phát âm quốc tế là "chi"; thế rồi diễn đàn Toán học VN lại nói nó được phát âm tiếng Việt là "si". Thế nên thôi, tôi quyết định ko đọc tên, mà viết ký hiệu như bên trên.
Lúc được học, hoặc search Google, bạn có thể thấy rằng phân phối $\chi^2$ này nhận được bằng cách lấy tổng của bình phương của $k$ mẫu ngẫu nhiên độc lập được lấy mẫu từ phân phối chuẩn tắc. Và rồi ở đâu cũng vậy, bộp 1 phát, chúng ta được đập ngay vào mặt 1 công thức hàm mật độ xác suất nhìn đúng là vãi lúa. Vậy làm thế nào để nhớ được cái của nợ này?
\[f(x) = \frac{e^{\frac{-x} {2}}x^{\frac{\nu} {2} - 1}} {2^{\frac{\nu} {2}}\Gamma(\frac{\nu} {2}) } \;\;\;\;\;\;\; \mbox{với} \; x \ge 0\]
Đối vs tôi, cách đơn giản nhất là "ko cần nhớ!". Như bên trên tôi đã nói, Hằng số chuẩn hỏa NormConst có trong hàm mật độ xác suất chẳng qua cũng chỉ là 1 hằng số được nhân thêm vào để hàm mật độ xác suất tích lũy có tích phân toàn cục bằng 1 mà thôi. Ta chỉ cần nhớ Kernel là có thể ra được mọi vấn đề! Do vậy, sau đây là cách mà tôi sử dụng để nhớ cái của nợ kia mỗi lần cần dùng đến. (Đương nhiên nếu làm nhiều, thuộc được thì sẽ nhớ ra ngay mà ko cần phải xử lý cồng kềnh như này)
Đầu tiên, như theo định nghĩa của phân phối $\chi^2$, chúng là "tổng bình phương" của nhiều biến ngẫu nhiên độc lập được lấy mẫu từ phân phối chuẩn tắc $Norm(\mu=0,\sigma^2=1)$. Nên giả sử, ta có điều kiện lấy mẫu $Y=X^2$ với $X\sim Norm(\mu=0,\sigma^2=1)=\frac{1}{\sqrt{2\pi}}exp\left(-\frac{x^2}{2}\right)$
Ta nhận thấy vì $Y=X^2$ nên $P(Y<y=0)=0$
Nên, với $y\ge0$, ta có hàm mật độ xác suất tích lũy:
\[P\left( {Y < y} \right) = P\left( {{X^2} < y} \right) = P\left( {\left| X \right| < \sqrt y } \right) = P\left( { - \sqrt y < X < \sqrt y } \right)\]
Bỏ qua tất cả các thành phần hằng số, chỉ xét Kernel, cộng thêm hàm dưới dấu tích phân là hàm chẵn, nên ta được:
\[P\left( {Y < y} \right) = \int\limits_{ - \sqrt y }^{\sqrt y } {\frac{1}{{\sqrt {2\pi } }}{e^{ - \frac{{{x^2}}}{2}}}} \propto \int\limits_0^{\sqrt y } {{e^{ - \frac{{{x^2}}}{2}}}dx} \]
Bên trên là công thức hàm tích lũy xác suất, hàm này liên tục và có đạo hàm tại mọi điểm trong miền lấy tích phân. Thế nên, lấy đạo hàm của hàm tích lũy này, ta sẽ thu được kết quả chính là hàm mật độ xác suất của phân phối $\chi^2$.
\[{f_Y}(y) = \frac{d}{{dy}}P\left( {Y < y} \right) \propto \frac{d}{{dy}}\left( {\int\limits_0^{\sqrt y } {{e^{ - \frac{{{x^2}}}{2}}}dx} } \right)\]
Đạo hàm cả cái tích phân này như nào? Trong giải tích 1 của Toán cao cấp, chúng ta có hệ quả khá đẹp:
\[\frac{d}{{dx}}\left[ {\int\limits_0^x {f(u)du} } \right] = f(x)\]
Thật ra thì chứng minh điều này khá đơn giản, học sinh THPT cũng có thể chứng minh được. Cụ thể giả sử $F$ là nguyên hàm của $f$, ta sẽ có kết quả:
\[\int\limits_0^x {f(u)du} = F(x) - F(0) \Rightarrow \frac{d}{{dx}}\left[ {\int\limits_0^x {f(u)du} } \right] = \frac{d}{{dx}}\left[ {F(x) - F(0)} \right] = \frac{{dF(x)}}{{dx}} = f(x)\]
Điều này xảy ra vì $F(0)$ là một hằng số. Khá là ez, học xong bài Nguyên hàm ở THPT phát là hiểu ngay được! OK, áp dụng kết quả này, tiến hành đạo hàm Hàm tích lũy xác suất, ta được:
\[{f_Y}(y) \propto \frac{d}{{dy}}\left( {\int\limits_0^{\sqrt y } {{e^{ - \frac{{{x^2}}}{2}}}dx} } \right) = {e^{ - \frac{{{{\left( {\sqrt y } \right)}^2}}}{2}}}.\frac{{d\left( {\sqrt y } \right)}}{{dy}} \propto {e^{ - \frac{y}{2}}}.{y^{ - \frac{1}{2}}}\]
Nếu lấy mẫu $k$ lần, ta chỉ việc thay $y^{-{1}{2}}$ bởi $y^{-{k}{2}}$. Vậy là ta đã thu được Kernel trong hàm mật độ xác suất của phân phối $\chi^2$. Còn Hằng số chuẩn hóa NormConst thì mặc xác nó; lúc nào cần thì Google search; còn ko thì ta vẫn cứ lấy mẫu được vì đã có Kernel rồi.
Phân phối Student.
Phân phối Student $t$ thu được bằng cách lấy mẫu theo biểu thức $T_n=\frac{N}{\sqrt{\frac{\chi^2}{n}}}$. Với tử số là giá trị được lấy mẫu từ phân phối chuẩn tắc $Norm(\mu=0,\sigma^2=1)$ và tử số trong căn thức ở mẫu số được lấy mẫu theo phân phối $\chi^2$. Phân phối này được sử dụng trong trường hợp số mẫu kiểm định nhỏ hơn 30. Khi số mẫu lớn hơn hoặc bằng 30, người ta sẽ xấp xỉ thống kê về theo phân phối Gaussian.
Nói chung, phân phối này cũng có 1 hàm mật độ xác suất còn vãi lúa hơn cả phân phối $\chi^2$. Tôi cũng ko nhớ được cái hàm mật độ đó; cách lần mò ra được cái hàm mật độ đó cũng thuộc dạng khá khùm khoằm; cộng thêm việc chưa sử dụng nó bao giờ nên cũng ko nhớ cái cách sinh ra Kernel của nó.
Nói chung, phân phối này cũng có 1 hàm mật độ xác suất còn vãi lúa hơn cả phân phối $\chi^2$. Tôi cũng ko nhớ được cái hàm mật độ đó; cách lần mò ra được cái hàm mật độ đó cũng thuộc dạng khá khùm khoằm; cộng thêm việc chưa sử dụng nó bao giờ nên cũng ko nhớ cái cách sinh ra Kernel của nó.
Tóm lại.
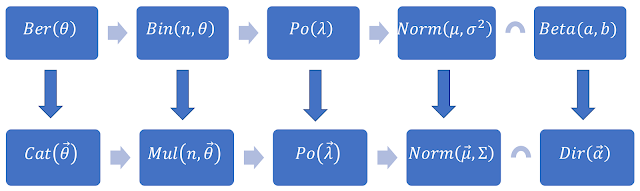
Vậy là chúng ta đã đi qua được gần hết quá trình xấp xỉ nhau, tổng quát nhau giữa các phân phối xác suất thường gặp nhất trong quá trình nghiên cứu Machine Learning. Nói chung thì quanh đi quẩn lại, chỉ có 2 cách tổng quát hóa phân phối xác suất này thành phân phối xác suất tổng quát hơn. Bắt đầu đều từ việc tung đồng xu của phân phối Bernoully, rồi kết thúc tại trung tâm của mọi thứ là phân phối Gaussian.
Thế còn 2 cái phân phối ở rìa ngoài cùng: phân phối Beta và phân phối Dirichlet? Bạn sẽ thấy rằng tôi ko dùng dấu mũi tên để biểu diễn mối quan hệ giữa chúng và phân phối đằng trước. Do vậy, chúng ko thể gọi là tổng quát hơn so với các phân phối xác suất mà chúng ta đã trải qua được. Tuy nhiên, chúng lại rất quan trọng, vì chúng biểu thị phân phối xác suất của các tham số của các phân phối xác suất mà chúng ta đã trải qua. Những điều này sẽ được tôi trình bày chi tiết trong bài viết sau, bài viết cuối cùng của seri này.
Trước khi kết thúc, tặng các bạn 1 sơ đồ Xác suất. Nhìn nó còn phê hơn tất cả các sơ đồ Hóa học mà hồi trước ôn thi đại học. Tôi lấy sơ đồ đó tại đây.



Nhận xét
Đăng nhận xét