Quan hệ giữa các phân phối xác suất thông dụng nhất: Beta và Dirichlet không giống Gaussian!
Kết thúc loạt bài viết nói về quan hệ giữa các phân phối xác suất thông dụng nhất, cũng như vài thủ thuật nhớ những thứ liên quan, trong bài viết cuối này, tôi sẽ nói về 2 phân phối xác suất có quan hệ với Gaussian 1 chiều và Gaussian nhiều chiều. Nhưng, chúng không phải quan hệ tổng quát hóa như những bài trước, vì 2 phân phối này biểu diễn loại biến ngẫu nhiên khác với các phân phối trước!
Beta và Dirichlet là 2 phân phối xác suất tương ứng cho với trường hợp biến ngẫu nhiên 1 chiều và nhiều chiều. Dirichlet là phân phối tổng quát của Beta. Khi nghiên cứu, về chúng, bạn sẽ biết được rằng 2 phân phối này dùng để mô tả biến động cho các tham số của những phân phối xác suất tương ứng mà chúng liên hợp.
\[ker(binomial).ker(beta)=\left[\theta^k.(1-\theta)^{n-k}\right]\left[\theta^{\alpha-1}.(1-\theta)^{\beta-1}\right]=\theta^{k+\alpha-1}.(1-\theta)^{n+\beta-k-1}\]
Nói chung, kết quả vẫn là dạng $\theta$ mũ j đó, nhân với $1-\theta$ mũ j đó; vẫn giống với hình dạng kernel của cả Binomial và Beta. Bạn cũng có thể thấy điều này cũng sẽ xảy ra tương tự như khi ta nhận kernel của Multinomial và Dirichlet lại với nhau.
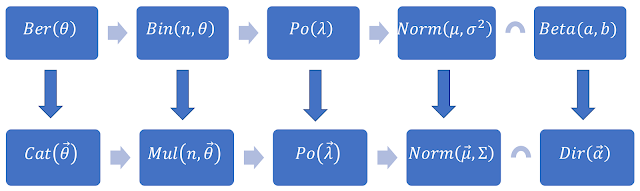
Lại thấy rằng Binomial là dạng tổng quát của Bernoully, nên Beta cũng là liên hợp của Bernoully. Tương tự, Dirichlet cũng là liên hợp của Categorical. Thế nên, lại nhìn vào cái hình quen thuộc ở trên, ta thấy rằng Beta là liên hợp cho những phân phối xác suất mo tả biến ngẫu nhiên 1 chiều; còn Dirichlet là tương ứng cho trường hợp biến ngẫu nhiên nhiều chiều.
Thế còn Beta với Gaussian thì có quan hệ như nào? Một cách trực giác và dễ nhớ, theo tư tưởng của Định lý giới hạn trung tâm, các mẫu lấy từ các phân phối xác suất sau càng nhiều lần sẽ cho ra một phân phối xác suất tiến về Gaussian! Do đó ta có thể đoán rằng giữa Gaussian và Beta, tuy không phải là tổng quát của nhau , nhưng cũng có một mối quan hệ tương quan nào đó giúp ta dễ nhớ một chút (vì Beta không phải lúc nào cũng đối xứng, còn Gaussian thì luôn đối xứng).
Thật sự thì $Beta(b, b)$ sẽ hội tụ về Gaussian khi $b\to\infty$! Điều này nghe qua có vẻ tin tưởng được, vì Beta sẽ có phân phối đối xứng nếu $\alpha = \beta$; và khi 2 số này bằng nhau và tiến về $\infty$ thì cũng ko ngoại trừ khả năng này.
Trước tiên, ta cứ check thực nghiệm xem sao. Tôi sẽ tiến hành lẫy 1000 mẫu theo phân phối Beta, sau đó show kết quả lên xem nó ra hình dạng j. Nếu thấy nó có hình đối xứng hình chuông như Gaussian thì ta có thể tạm tin được nhận định trên. Điều này khá đơn giản, dùng numpy, ta có thể lấy 1000 mẫu theo phân phối Beta, sau đó dùng matplotlib để visualize kết quả dưới dạng histogram để xem đồ thị mật độ xác suất như nào.
Có vẻ khá giống Gaussian. Bạn có thể kiểm tra thêm nhiều trường hợp với các giá trị $b$ thay đổi (bên trên mình thử $b=4$), lấy thêm nhiều mẫu hơn (bên trên mình lấy 1000 mẫu) và thay đổi interval của histogram (bên trên mình để bin = 100).
Sau khi đã kiểm nghiệm bằng code, bây giờ tôi sẽ trình bày việc chứng minh $Beta(b,b)$ sẽ hội tụ về Gaussian khi $b\to\infty$. Pha này ko thích thú lắm như pha code ở trên. Cụ thể, ta sẽ chứng minh hàm mật độ xác suất của một biến ngẫu nhiên $X\sim B(b,b)$ sẽ hội tụ về hình dạng hàm mật độ xác suất của Gaussian khi $b\to\infty$, với $0<x<1$. Hàm mật độ khi đó là:
\[X\sim B(b,b)\Rightarrow f_X(x)=\frac{\Gamma(2b).x^{b-1}.(1-x)^{b-1}}{\Gamma(b).\Gamma(b)}\]
Tra Wikipedia, chúng ta tính được ngay Beta trong trường hợp này sẽ có kỳ vọng $E[X]=\mu=\frac{1}{2}$ và phương sai $V[X]=\sigma^2=\frac{1}{4(2b+1)}$. Thực hiện chuẩn hóa thống kê theo công thức quen thuộc $Y = \frac{X-\mu}{\sigma}$, ta sẽ thu được biến ngẫu nhiên $Y=g(X)=\frac{X-\mu}{\sigma}=2\sqrt{2b+1}\left(X-\frac{1}{2}\right)$. $g$ là 1 song ánh từ tập $x\in(0;1)\to y\in(-\sqrt{2b+1};\sqrt{2b+1})$
Do đó, ánh xạ ngược lại, ta được $X=g^{-1}(Y)=\frac{Y}{2\sqrt{2b+1}}+\frac{1}{2}$.
\[\Rightarrow\frac{dX}{dY}=\frac{1}{2\sqrt{2b+1}}\]
Thay vào hàm mật độ xác suất của X, ta được:
\[f_Y(y)=\frac{1}{2\sqrt{2b+1}}.f_X\left(\frac{y}{2\sqrt{2b+1}}+\frac{1}{2}\right)\]
\[=\frac{1}{2\sqrt{2b+1}}.\frac{\Gamma(2b)}{\Gamma^2(b)}\left(\frac{1}{2}+\frac{y}{2\sqrt{2b+1}}\right)^{b-1}.\left(\frac{1}{2}-\frac{y}{2\sqrt{2b+1}}\right)^{b-1}=\frac{1}{2\sqrt{2b+1}}.\frac{\Gamma(2b)}{\Gamma^2(b)}.\left(\frac{1}{4}-\frac{y^2}{4(2b+1)}\right)\]
Bây giờ, vì có hàm Gamma, nên ta tiếp tục sử dụng ước lượng Stirling nhằm phá dấu giai thừa trong hàm Gamma. Cụ thể $\Gamma(z)=\sqrt{\frac{2\pi}{x}}(\frac{z}{e})^z.\left(1+O(\frac{1}{z})\right)$. Tiếp tục biến đổi, ta được:
\[f_Y(y)=\frac{1}{2\sqrt{2b+1}}\frac{\frac{2\pi}{2b}(\frac{2b}{e})^{2b}}{\frac{2\pi}{b}(\frac{b}{e})^{2b}}\left[1+O\left(\frac{1}{b}\right)\right]\left[\frac{1}{4}-\frac{y^2}{4(2b+1)}\right]\]
\[=\frac{b}{\sqrt{2b}.\sqrt{2b+1}}\frac{2^{2b}}{2\sqrt{2\pi}}.\left[1+O\left(\frac{1}{b}\right)\right]\left[\frac{1}{4}-\frac{y^2}{4(2b+1)}\right]\]
\[=\frac{1}{\sqrt{2\pi}}\left(1-\frac{y^2}{2b+1}\right).\left[1+O\left(\frac{1}{b}\right)\right]=\frac{1}{\sqrt{2\pi}}\exp(-\frac{y^2}{2}).\left[1+O\left(\frac{1}{b}\right)\right]\]
Vậy ta thu được kết quả xấp xỉ cuối cùng có hình dạng chính là hàm mật độ xác suất của phân phối Gaussian (thêm 1 ít nhiễu sẽ bị tiễu trừ khi $b\to+\infty$. Chuẩn luôn. Bên trên ta đã chuẩn hóa phân phối Beta này về dạng chuẩn; sau khi biến đổi, ta lại thu được kết quả là phân phối Gaussian chuẩn tắc. Do vậy, ta đã có thể đưa ra nhận định $Beta(b,b)$ sẽ hội tụ về Gaussian khi $b\to\infty$. Về Gaussian thôi nhé, ko phải về Gaussian chuẩn tắc đâu! X chỉ về Gaussian, còn Y (dạng chuẩn hóa của X) thì mới về Gaussian chuẩn tắc! Và cũng chỉ $Beta(b,b)$ thôi, tức là khi $\alpha=\beta$; chứ còn Beta không giống Gaussian, không cái nào là tổng quát của nhau cả!
Quan hệ với Gaussian.
Ở đây xuất hiện khái niệm phân phối liên hợp. Nếu bạn chưa hiểu thế nào là 2 phân phối xác suất liên hợp nhau thì có thể hiểu theo cách đơn giản rằng khi đem nhân 2 kernel của chúng với nhau, ta thu được kết quả có hình dạng tương tự với cả 2 kernel ban đầu. Ví dụ như nếu bạn nhân kernel của Beta với Binomial thì bạn sẽ được một biểu thức cũng có hình dạng na ná với cả kernel của Beta và Binomial:\[ker(binomial).ker(beta)=\left[\theta^k.(1-\theta)^{n-k}\right]\left[\theta^{\alpha-1}.(1-\theta)^{\beta-1}\right]=\theta^{k+\alpha-1}.(1-\theta)^{n+\beta-k-1}\]
Nói chung, kết quả vẫn là dạng $\theta$ mũ j đó, nhân với $1-\theta$ mũ j đó; vẫn giống với hình dạng kernel của cả Binomial và Beta. Bạn cũng có thể thấy điều này cũng sẽ xảy ra tương tự như khi ta nhận kernel của Multinomial và Dirichlet lại với nhau.
Lại thấy rằng Binomial là dạng tổng quát của Bernoully, nên Beta cũng là liên hợp của Bernoully. Tương tự, Dirichlet cũng là liên hợp của Categorical. Thế nên, lại nhìn vào cái hình quen thuộc ở trên, ta thấy rằng Beta là liên hợp cho những phân phối xác suất mo tả biến ngẫu nhiên 1 chiều; còn Dirichlet là tương ứng cho trường hợp biến ngẫu nhiên nhiều chiều.
Thế còn Beta với Gaussian thì có quan hệ như nào? Một cách trực giác và dễ nhớ, theo tư tưởng của Định lý giới hạn trung tâm, các mẫu lấy từ các phân phối xác suất sau càng nhiều lần sẽ cho ra một phân phối xác suất tiến về Gaussian! Do đó ta có thể đoán rằng giữa Gaussian và Beta, tuy không phải là tổng quát của nhau , nhưng cũng có một mối quan hệ tương quan nào đó giúp ta dễ nhớ một chút (vì Beta không phải lúc nào cũng đối xứng, còn Gaussian thì luôn đối xứng).
Thật sự thì $Beta(b, b)$ sẽ hội tụ về Gaussian khi $b\to\infty$! Điều này nghe qua có vẻ tin tưởng được, vì Beta sẽ có phân phối đối xứng nếu $\alpha = \beta$; và khi 2 số này bằng nhau và tiến về $\infty$ thì cũng ko ngoại trừ khả năng này.
Trước tiên, ta cứ check thực nghiệm xem sao. Tôi sẽ tiến hành lẫy 1000 mẫu theo phân phối Beta, sau đó show kết quả lên xem nó ra hình dạng j. Nếu thấy nó có hình đối xứng hình chuông như Gaussian thì ta có thể tạm tin được nhận định trên. Điều này khá đơn giản, dùng numpy, ta có thể lấy 1000 mẫu theo phân phối Beta, sau đó dùng matplotlib để visualize kết quả dưới dạng histogram để xem đồ thị mật độ xác suất như nào.
Có vẻ khá giống Gaussian. Bạn có thể kiểm tra thêm nhiều trường hợp với các giá trị $b$ thay đổi (bên trên mình thử $b=4$), lấy thêm nhiều mẫu hơn (bên trên mình lấy 1000 mẫu) và thay đổi interval của histogram (bên trên mình để bin = 100).
Sau khi đã kiểm nghiệm bằng code, bây giờ tôi sẽ trình bày việc chứng minh $Beta(b,b)$ sẽ hội tụ về Gaussian khi $b\to\infty$. Pha này ko thích thú lắm như pha code ở trên. Cụ thể, ta sẽ chứng minh hàm mật độ xác suất của một biến ngẫu nhiên $X\sim B(b,b)$ sẽ hội tụ về hình dạng hàm mật độ xác suất của Gaussian khi $b\to\infty$, với $0<x<1$. Hàm mật độ khi đó là:
\[X\sim B(b,b)\Rightarrow f_X(x)=\frac{\Gamma(2b).x^{b-1}.(1-x)^{b-1}}{\Gamma(b).\Gamma(b)}\]
Tra Wikipedia, chúng ta tính được ngay Beta trong trường hợp này sẽ có kỳ vọng $E[X]=\mu=\frac{1}{2}$ và phương sai $V[X]=\sigma^2=\frac{1}{4(2b+1)}$. Thực hiện chuẩn hóa thống kê theo công thức quen thuộc $Y = \frac{X-\mu}{\sigma}$, ta sẽ thu được biến ngẫu nhiên $Y=g(X)=\frac{X-\mu}{\sigma}=2\sqrt{2b+1}\left(X-\frac{1}{2}\right)$. $g$ là 1 song ánh từ tập $x\in(0;1)\to y\in(-\sqrt{2b+1};\sqrt{2b+1})$
Do đó, ánh xạ ngược lại, ta được $X=g^{-1}(Y)=\frac{Y}{2\sqrt{2b+1}}+\frac{1}{2}$.
\[\Rightarrow\frac{dX}{dY}=\frac{1}{2\sqrt{2b+1}}\]
Thay vào hàm mật độ xác suất của X, ta được:
\[f_Y(y)=\frac{1}{2\sqrt{2b+1}}.f_X\left(\frac{y}{2\sqrt{2b+1}}+\frac{1}{2}\right)\]
\[=\frac{1}{2\sqrt{2b+1}}.\frac{\Gamma(2b)}{\Gamma^2(b)}\left(\frac{1}{2}+\frac{y}{2\sqrt{2b+1}}\right)^{b-1}.\left(\frac{1}{2}-\frac{y}{2\sqrt{2b+1}}\right)^{b-1}=\frac{1}{2\sqrt{2b+1}}.\frac{\Gamma(2b)}{\Gamma^2(b)}.\left(\frac{1}{4}-\frac{y^2}{4(2b+1)}\right)\]
Bây giờ, vì có hàm Gamma, nên ta tiếp tục sử dụng ước lượng Stirling nhằm phá dấu giai thừa trong hàm Gamma. Cụ thể $\Gamma(z)=\sqrt{\frac{2\pi}{x}}(\frac{z}{e})^z.\left(1+O(\frac{1}{z})\right)$. Tiếp tục biến đổi, ta được:
\[f_Y(y)=\frac{1}{2\sqrt{2b+1}}\frac{\frac{2\pi}{2b}(\frac{2b}{e})^{2b}}{\frac{2\pi}{b}(\frac{b}{e})^{2b}}\left[1+O\left(\frac{1}{b}\right)\right]\left[\frac{1}{4}-\frac{y^2}{4(2b+1)}\right]\]
\[=\frac{b}{\sqrt{2b}.\sqrt{2b+1}}\frac{2^{2b}}{2\sqrt{2\pi}}.\left[1+O\left(\frac{1}{b}\right)\right]\left[\frac{1}{4}-\frac{y^2}{4(2b+1)}\right]\]
\[=\frac{1}{\sqrt{2\pi}}\left(1-\frac{y^2}{2b+1}\right).\left[1+O\left(\frac{1}{b}\right)\right]=\frac{1}{\sqrt{2\pi}}\exp(-\frac{y^2}{2}).\left[1+O\left(\frac{1}{b}\right)\right]\]
Vậy ta thu được kết quả xấp xỉ cuối cùng có hình dạng chính là hàm mật độ xác suất của phân phối Gaussian (thêm 1 ít nhiễu sẽ bị tiễu trừ khi $b\to+\infty$. Chuẩn luôn. Bên trên ta đã chuẩn hóa phân phối Beta này về dạng chuẩn; sau khi biến đổi, ta lại thu được kết quả là phân phối Gaussian chuẩn tắc. Do vậy, ta đã có thể đưa ra nhận định $Beta(b,b)$ sẽ hội tụ về Gaussian khi $b\to\infty$. Về Gaussian thôi nhé, ko phải về Gaussian chuẩn tắc đâu! X chỉ về Gaussian, còn Y (dạng chuẩn hóa của X) thì mới về Gaussian chuẩn tắc! Và cũng chỉ $Beta(b,b)$ thôi, tức là khi $\alpha=\beta$; chứ còn Beta không giống Gaussian, không cái nào là tổng quát của nhau cả!



Em ơi, viết tiếp nội dung này đi em
Trả lờiXóasr giờ mình ko có thời gian để viết bài chuyên sâu về kỹ thuật nữa rồi :v
Xóa