Tào lao: Đơn vị đo của Entropy là "NÁT"

Đây là 1 bài viết khá tào lao về 1 khái niệm xuất hiện ở khá nhiều lĩnh vực kỹ thuật khác nhau. Hồi kỳ 1 năm 1 đại học, học Vật Lý đại cương về Cơ học, thầy Nguyễn Huyền Tụng đã có nói đến nó; kỳ 2 năm 1 học Nhiệt học cũng có nói đến nó; kỳ 1 năm 2 học cái môn Vật Lý điện tử khốn kiếp của thầy Lê Tuấn cũng lại nói đến nó; kỳ 2 năm 3 học Lý thuyết thông tin của thầy Đặng Văn Chuyết cũng lại nói đến nó. Và từ lúc đó trở đi, mình đã tự ngộ ra được trong bất cứ lĩnh vực củ cải nào của đời sống này cũng đều có sự xuất hiện của nó. Và nó ko phải j khác, chính là "ENTROPY".

Nếu ko biết Entropy nghĩa là j, bạn có thể Google search xem sao; còn theo như tôi hiểu, thì Entropy là đại lượng biểu thị "độ bất ngờ" của các đại lượng xuất hiện theo thời gian. Công thức tổng quát của nó trong mọi lĩnh vực ký thuật đều nôm na biểu diễn như sau:

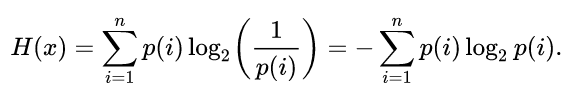Ảnh này tôi lấy tạm trên Wikipedia, vì mới cài lại Linux, chưa tìm cách gõ công thức toán trên blog được.

OK, có thể thấy rằng ký hiệu tổng sigma ở trên hoàn toàn có thể thay thế bằng ký hiệu lấy tích phân trong một miền xác định của biến số nếu biến số đó là một đại lượng liên tục. Còn trong công thức tổng quát tạm lấy trên, i là một đại lượng có các giá trị rời rạc, do đó công thức sử dụng dấu sigma.

Theo như tôi nhớ thì hồi đó, thầy Chuyết có giải thích với lớp bọn tôi đại khái như sau: nếu có 1 dòng tin đến liên tục trên 1 kênh truyền, nếu càng khó đoán trước được giá trị của các gói tin đang sắp đến, thì Entropy càng cao; và ngược lại. Nghĩa là Entropy biểu thị cho "độ bất ngờ" của các tin đang đến. Nếu Entropy tính được càng thấp, chứng tỏ nguồn tin càng ít gây ra bất ngờ cho ta, do đó ta càng dễ đoán được giá trị của tin đang chuyển đến; và ngược lại.

Đây là cách giải thích khá dễ hiểu, vì chí ít thì tôi cũng nhớ nó cho đến tận bây giờ; và dựa vào cách giải thích này, tôi có thể nhanh chóng hiểu được ý nghĩa của bất cứ công thức Entropy nào mà mình bắt gặp sau đó; tiêu biểu chính là Cross - Entropy trong mô hình Logistic Regression nói chung của Machine Learning. 

Ngoài cách hiểu đơn giản đó ra, hôm nay, tình cờ vào xem facebook của cậu em (khá giỏi về Machine Learning), tôi thấy cậu ấy có một mô tả (bio) khá hay, cụ thể là "Entropy is measured in unit of 'nat'!". Đọc xong tôi mới nhớ ra bình thường cậu ấy rất hay dùng từ "nát" khi trao đổi và nói chuyện vs tôi; kiểu như "môn này em khá nát", "hôm nay thi cũng ko nát lắm", "bên công ty thúc deadline, nát rồi anh", ... Về cơ bản, cách hiểu này đúng là khá tếu và sáng tạo.

Trong Machine Learning, cụ thể là Logistic Regression và Neural Network, một mô hình có Cross - Entropy càng cao, nghĩa là giá trị Coss Function (hàm mất mát) càng lớn, đồng nghĩa với việc model đưa ra càng ko có hiệu quả ngay trên bộ dữ liệu Training Set, tức là model càng "nát"! Mục tiêu của người thiết kế thuật toán cũng như mô hình Machine Learning là tìm ra mô hình nào tối ưu được Coss Funtion, tức là giảm độ nát của mô hình/thuật toán. Mô hình càng nát thì càng vất đi.

Có thể thấy rằng trong mọi khía cạnh của đời sống, ta cũng đều phải có sự góp mặt của thủ tục "dự đoán"! Dự đoán càng trúng nhiều thì nghĩa là càng ít nát; còn nếu dự đoán càng trượt, tức là độ bất ngờ lên càng cao, có nghĩa là ta càng trở lên nát; và mục tiêu của ta là phải giảm độ nát xuống.